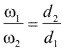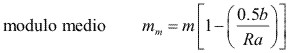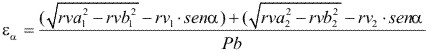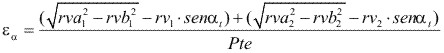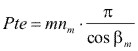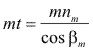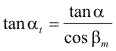3.1.4.- Engranajes Cónicos.
Engranajes Cónicos (Recuperado de https://youtu.be/vxn4Z_JvsMM)
a).- Generalidades.
Los engranajes cónicos, se emplean para transmitir movimientos de rotación, entre ejes concurrentes (O1, O2) Fig. 3.91
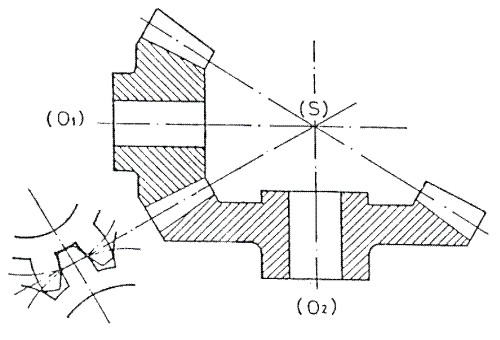
Fig. 3.91 Engranaje cónico.
Los cuerpos de los engranajes, son de forma troncocónica, con un vértice común (S), coincidiendo con el punto de intersección de los ejes.
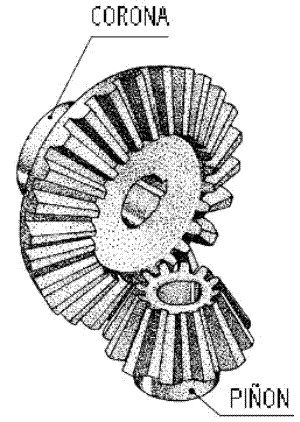
Fig. 3.92 Engranaje cónico de dientes rectos.
En el par de engranes cónicos al menor le llamaremos piñón y al mayor simplemente Corona o rueda.
Según sea la forma longitudinal de los dientes los engranajes cónicos pueden ser:
Engranes con dentado recto.
En los engranes cónicos con dentado recto, los flancos de los dientes son rectilíneos y en su prolongación convergen en el vértice (S) del cono. (Fig. 3.93)
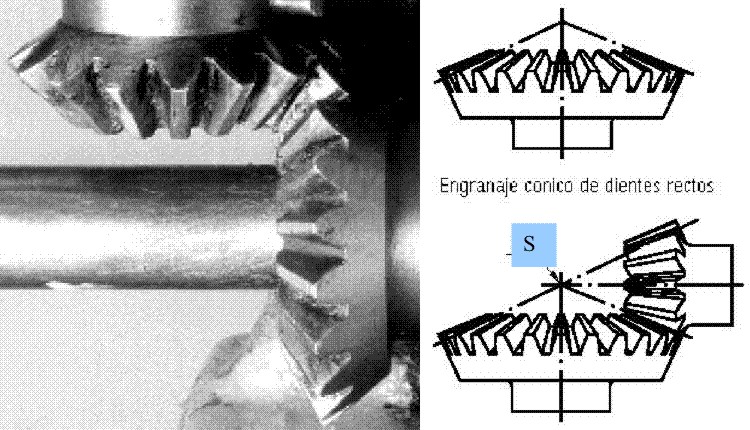
Fig. 3.93
Engrane con dentado helicoidal, espiral, etc.
En los engranes cónicos con dentado helicoidal, espiral, etc., los flancos de los dientes no convergen hacia el vértice (S) del cono. (Fig. 3.94)
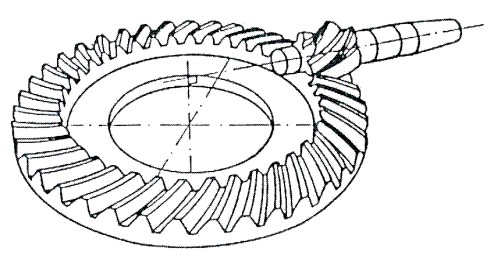
Fig. 3.94
b).- Engranaje Cónico con dientes rectos.
En un engrane cónico con dientes rectos distinguimos los siguientes elementos (Fig.3.95):
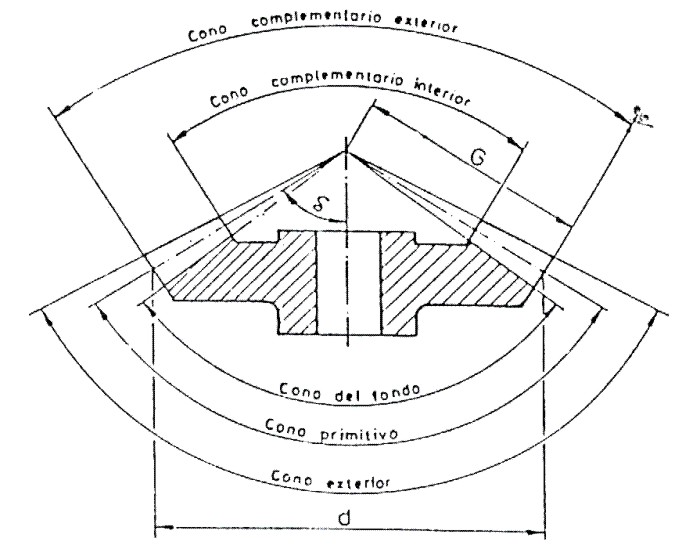
Fig. 3.95 Elementos del engrane cónico.
Cono primitivo: Es aquel que limita los puntos de tangencia entre los engranes.
Cono exterior: Es aquel que limita el diente exteriormente.
Cono del fondo: Es aquel que limita el diente interiormente.
Conos complementarios: Son aquellos que limitan el largo del diente, siendo sus generatrices perpendiculares a las del cono primitivo.
Angulo primitivo (
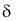 ): Es el ángulo formado por la generatriz (G) del cono primitivo y el eje del engrane.
): Es el ángulo formado por la generatriz (G) del cono primitivo y el eje del engrane.Diámetro primitivo (d): Corresponde al diámetro exterior de la base mayor del cono primitivo.
c).- Ángulo Primitivo (![]() ). Relación de transmisión (i). Ángulo que forman los ejes (
). Relación de transmisión (i). Ángulo que forman los ejes (![]() ).
).
En los engranajes cónicos (Fig. 3.96), el ángulo primitivo de la rueda (![]() 2), y del piñón (
2), y del piñón (![]() 1) están siempre en función de la relación de transmisión (i) y el valor del ángulo que forman los ejes del engranaje (
1) están siempre en función de la relación de transmisión (i) y el valor del ángulo que forman los ejes del engranaje (![]() )
)
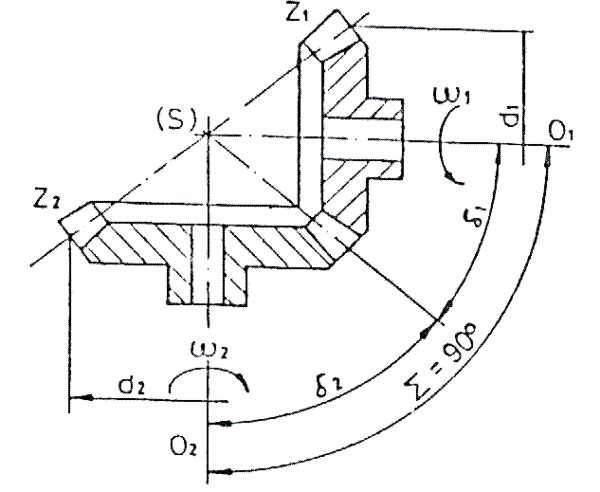
Fig. 3.96 Engranaje cónico ![]() = 90°.
= 90°.
Para demostrar la relación existente entre ángulos primitivos (![]() ), relación de transmisión (i) y el ángulo entre ejes (
), relación de transmisión (i) y el ángulo entre ejes (![]() ), se va a considerar un dispositivo de ruedas cónicas de fricción (Fig. 3.97)
), se va a considerar un dispositivo de ruedas cónicas de fricción (Fig. 3.97)
Dichas ruedas cónicas coinciden en dimensiones con los conos primitivos del engranaje en la figura 3.96
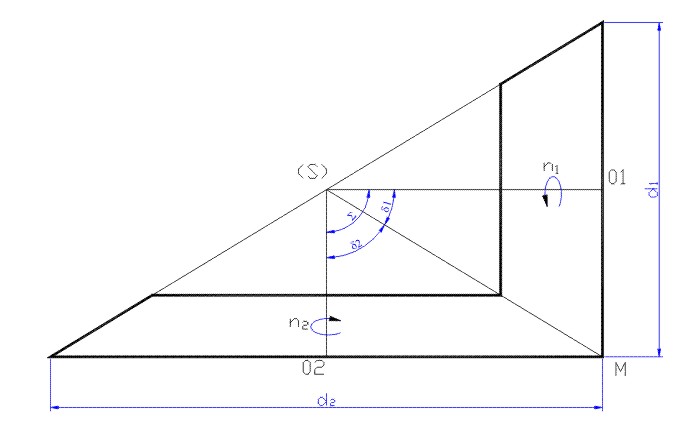
Fig. 3.97 Ruedas de fricción.
Si entre las ruedas cónicas de fricción, no existe deslizamiento, las velocidades tangenciales en el punto M son iguales, o sea:
![]()
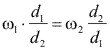
|
(4.1)
|
En este caso particular de ángulo entre ejes ![]() = 90°. los ángulos primitivos del piñón (
= 90°. los ángulos primitivos del piñón (![]() 1) y de la rueda (
1) y de la rueda (![]() 2) se determinan en función de:
2) se determinan en función de:
Los diámetros primitivos respectivos d1 y d2
Las velocidades angulares
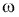 1 y
1 y 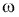 2
2El número de dientes respectivos z1 y z2 siendo.
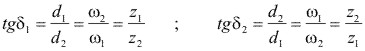
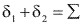 (4.2)
(4.2)
En el caso particular de ángulo entre ejes ![]() > 90° (Fig. 3.98) el ángulo primitivo del piñón se determina en función de:
> 90° (Fig. 3.98) el ángulo primitivo del piñón se determina en función de:
El ángulo entre ejes (
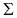 )
)El número de dientes del piñón y rueda z1 y z2
Siendo:
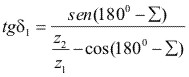 (4.3)
(4.3)
y en cuanto al ángulo primitivo de la rueda1, su valor sé determina en función de:
El ángulo entre ejes (
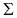 )
)El ángulo primitivo del piñón
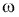 1
1Siendo:
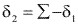 (4.4)
(4.4)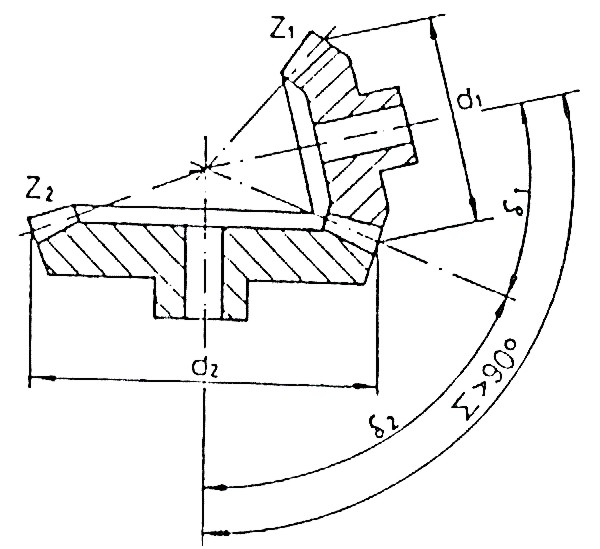
Fig. 3.98 Engranaje cónico
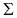 > 90°.
> 90°.
En el caso particular de ángulo entre ejes ![]() < 90° (Fig.3.99) el ángulo primitivo del piñón se determina en función de:
< 90° (Fig.3.99) el ángulo primitivo del piñón se determina en función de:
El ángulo entre ejes (
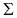 )
)El número de dientes del piñón y rueda z1 y z2
Siendo:
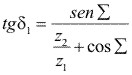 (4.5)
(4.5)
y en cuanto al ángulo primitivo de la rueda, su valor se determina en función de::
El ángulo entre ejes (
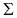 )
)El ángulo primitivo del piñón
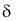 1
1Siendo:
 (4.6)
(4.6)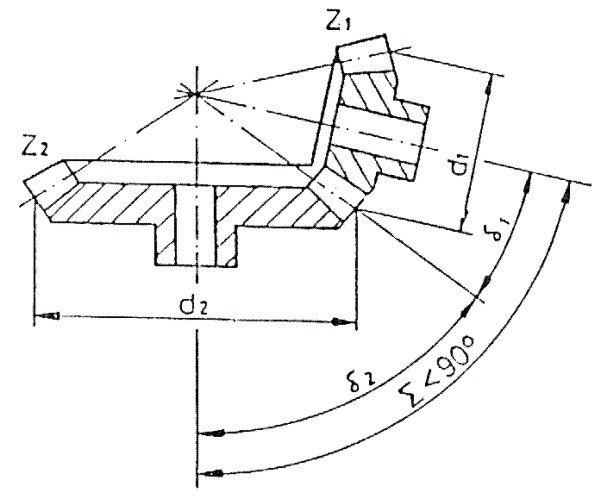
Fig. 3.99 Engranaje cónico exterior
 < 90°.
< 90°.
En el caso particular de engranaje interior con ![]() < 90° (Fig. 3.100) el ángulo primitivo del piñón se determina en función de:
< 90° (Fig. 3.100) el ángulo primitivo del piñón se determina en función de:
El ángulo entre ejes (
 )
)El número de dientes del piñón y rueda z1 y z2
Siendo:
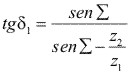 (4.7)
(4.7)
y en cuanto al ángulo primitivo de la rueda, su valor se determina en función de:
El ángulo entre ejes (
 )
)El ángulo primitivo del piñón
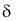 1
1Siendo:
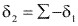 (4.8)
(4.8)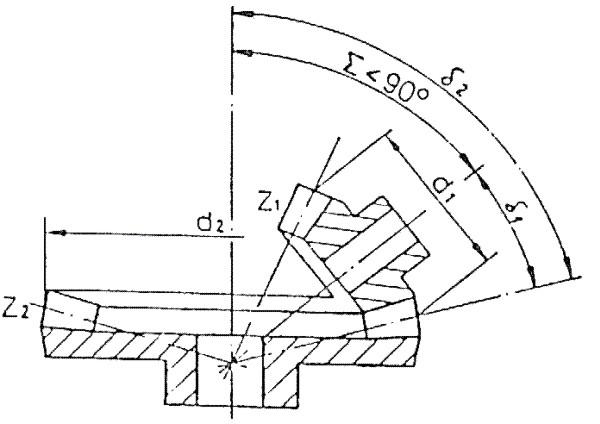
Fig. 3.100 Engranaje cónico interior
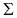 < 90°.
< 90°.
d).- Definiciones y relaciones fundamentales.
Además de los. elementos definidos en el apartado a).- en un engranaje cónico también se deben considerar (Fig.3.101)
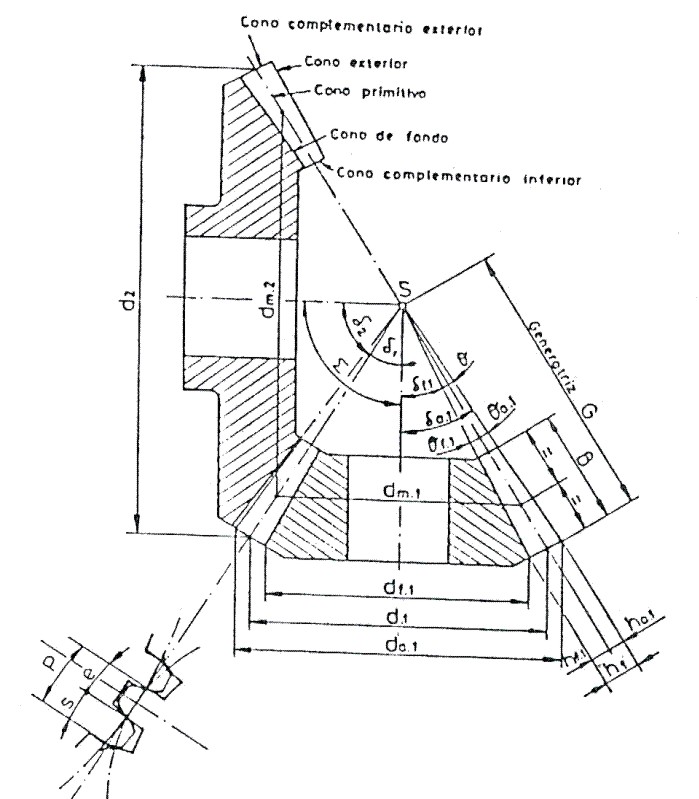
Fig. 3.101 Engranaje cónico con dentado recto.
Diámetro exterior (da): Corresponde al diámetro exterior de la base mayor del cono exterior.
Diámetro del fondo (df): Correspondiente a la base mayor del cono interior.
Módulo (m): En un engrane cónico, el módulo siempre corresponde al de la base mayor, y a éste se referirá en los cálculos, aunque en la longitud del diente existen varios módulos.
Longitud del diente (B): Se recomienda no sobrepasar un valor igual a 1/3 de la generatriz G. (B< 1,3 . G).
Angulo exterior (
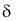 a): Es el ángulo formado por la superficie exterior del diente y el eje del engrane.
a): Es el ángulo formado por la superficie exterior del diente y el eje del engrane.Angulo del fondo (
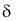 r): Es el ángulo formado por la superficie del fondo del diente y el eje del engrane.
r): Es el ángulo formado por la superficie del fondo del diente y el eje del engrane.Angulo de cabeza (
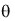 a): Llamado también de addendum y corresponde a la diferencia entre el ángulo exterior (
a): Llamado también de addendum y corresponde a la diferencia entre el ángulo exterior (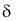 a) y el primitivo (
a) y el primitivo (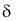 ).
).Angulo del pie (
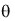 f): Llamado también dedendum y corresponde a la diferencia entre el ángulo primitivo (
f): Llamado también dedendum y corresponde a la diferencia entre el ángulo primitivo (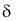 ) y el del fondo (
) y el del fondo (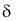 f).
f).Angulo de profundidad (
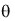 ): Corresponde a la suma del ángulo de cabeza (
): Corresponde a la suma del ángulo de cabeza (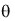 a) y el ángulo del pie (
a) y el ángulo del pie (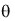 f).
f).
Relaciones fundamentales.
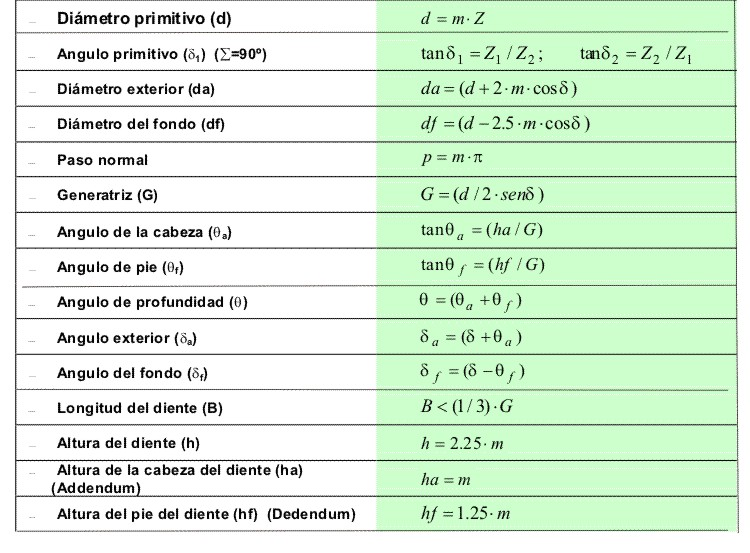
e).- Engranaje complementario de dientes rectos.
Al desarrollar los conos complementarios de vértices s1 y s2 sobre un plano (Fig. 3.102), se obtienen dos sectores circulares de centros S1 y S2 y los círculos primitivos d1 y d2 se desarrollaran según arcos de radios ![]() respectivamente.
respectivamente.
De esta forma se obtiene un engranaje de dos ruedas cilíndricas, llamadas ruedas complementarias de las ruedas cónicas. Al engranaje se le denomina: Engranaje complementario
El diámetro primitivo del piñón (dv1) de un engranaje complementario se determina en función de:
El diámetro primitivo del piñón d1
El ángulo primitivo del piñón
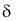 1
1Siendo:
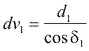 (4.9)
(4.9)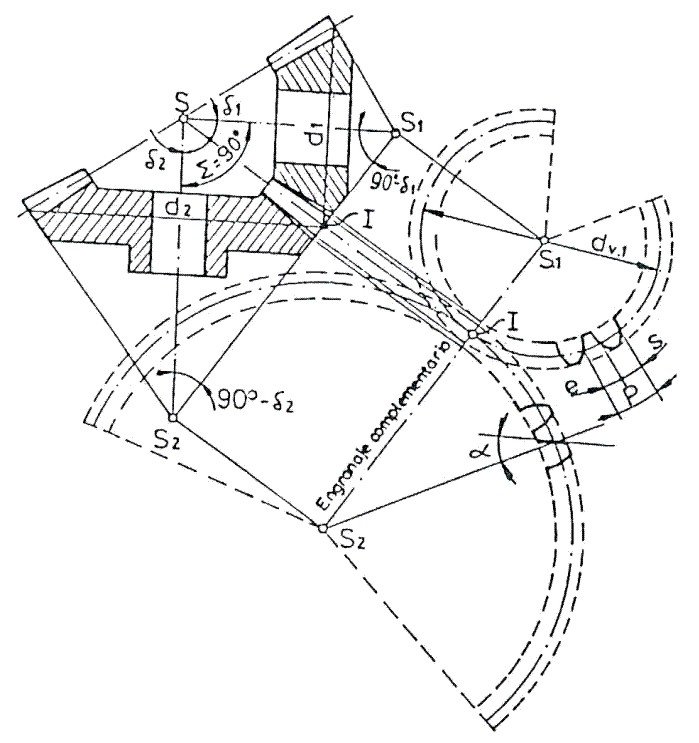
Fig. 3.102 Engranaje complementario.
y en cuanto al diámetro primitivo de la 'rueda (dv2) de un engranaje complementario, su valor, se determina en función de:
El diámetro primitivo del piñón d2
El ángulo primitivo del piñón
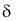 2
2Siendo:
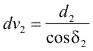 (4.10)
(4.10)
Las características de los dentados de las ruedas complementarías son las características nominales sobre los conos complementarios exteriores. Paso normal, módulo, ángulo de presión, etc.
En cuanto al número de dientes imaginario de un engranaje complementario, en el piñón se determina, en función de:
El diámetro primitivo del piñón complementario d1
El módulo m
o también, en función de:
El número de dientes del piñón Z1
El ángulo primitivo del piñón
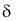 1
1Siendo:
 (4.11)
(4.11)
y en la rueda, el número de dientes imaginario se determina en función de:
El diámetro primitivo de la rueda complementaria dv2
Del módulo m
o también, en función de:
El número de dientes de la rueda Z2
El ángulo primitivo de la rueda
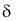 2
2Siendo:
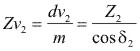 (4.12)
(4.12)
El engranaje complementario es particularmente interesante, porque permite estudiar los engranes cónicos con una aproximación suficiente, al considerado como un engrana recto.
De esta forma, todas las cuestiones relativas a la continuidad del engrane, interferencias, etc., pueden ser tratados considerando el engrane cónico, como un engrane de dientes rectos, con (Zv) dientes y módulo (m)
f).- Engranaje medio complementario.
Por causa de las relaciones de las fuerzas y del cálculo de la resistencia, se elige de modo conveniente el engrane medio complementario, en el centro del ancho de los dientes de la rueda cónica. (Fig. 3.103)
Como se ha explicado anteriormente, el módulo normalizado (m), se representa en el borde la base mayor del cono, por tanto:
|
(4.13)
|
Donde:
mm : Modulo en el centro del ancho del diente (mm)
m : Modulo normalizado (mm)
b : Ancho de los dientes
Ra : Radio de la rueda plana correspondiente (Fig. 3.104)
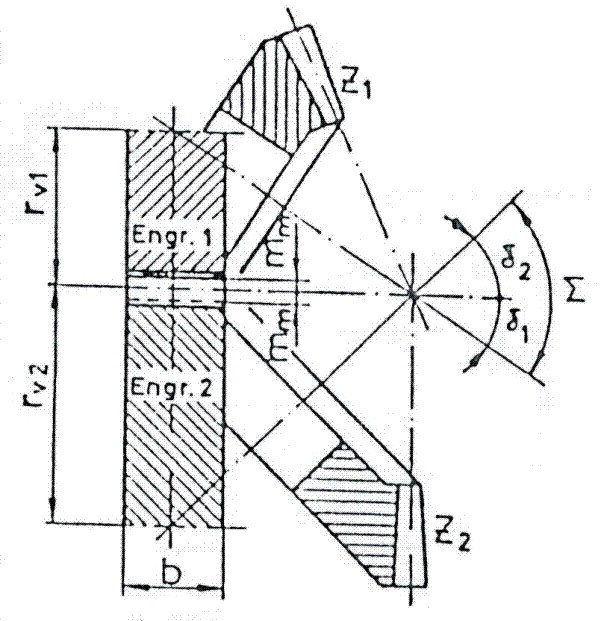
Fig. 3.103 Engranaje medio complementario.
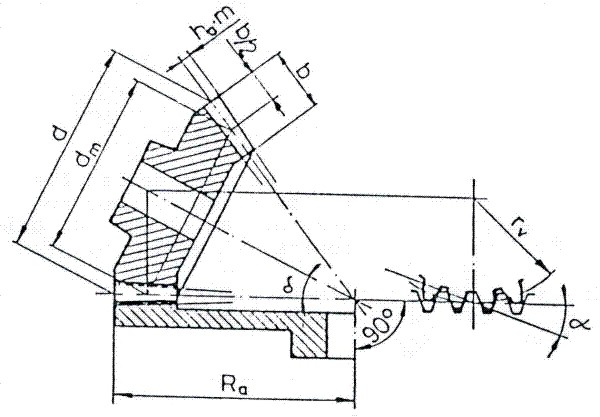
Fig. 3.104 Rueda cónica con la rueda plana correspondiente.
Relaciones fundamentales.
Numero de dientes complementarios
Donde:
Zv : Numero de dientes imaginario
Z : Numero de dientes del engrane
: Angulo primitivo
Diámetro primitivo de la rueda media complementaria,
Diámetro exterior de la rueda media complementaria.
Diámetro del circulo base de la rueda media complementaria.
Distancia imaginaria entre ejes (av).
g).- Relación de contacto.
|
(4.15)
|
Donde:
: Angulo de presión rv1 y rv2 : Radios primitivos del piñón y rueda complementaria rva1 y rva2 : Radios exteriores del piñón y rueda complementaria rvb1 y rvb2 : Radios bases del piñón y rueda complementaria Pb : Paso base del piñón y de la rueda complementaria
h).- Número de dientes para evitar la interferencia.
|
(4.16)
|
Donde:
Z' : Es el número de dientes limite de una rueda con dentado recto (para
0=20º Z'=17)
i).- Engranaje cónico de dentado inclinado o curvo.
Los engranes cónicos con dentado inclinado o curvo funcionan más silenciosas y con menos choques que los engranes con dentado recto. (Fig. 3.105).
Si los flancos de uno de los engranes tienen inclinación hacia la derecha los del otro lo tendrán hacia la izquierda:
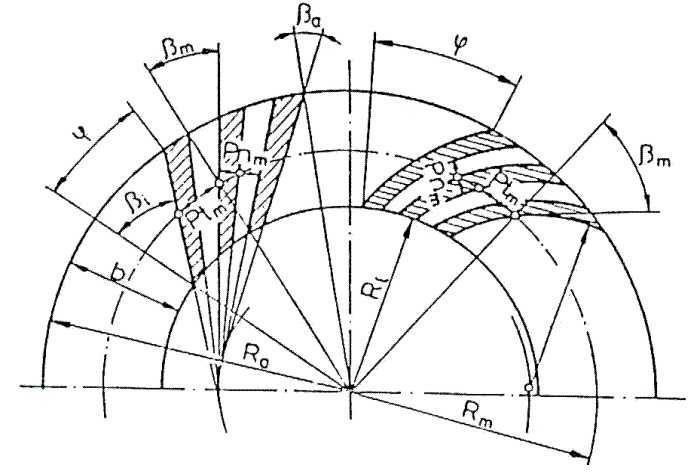
Fig. 3.105 Superficie exterior desarrollada de las ruedas cónicas de dientes inclinados y dientes curvos.
La inclinación de los dientes, en el medio del ancho de estos es ![]() m, en la periferia exterior es
m, en la periferia exterior es ![]() a y en la periferia interior
a y en la periferia interior ![]() i.
i.
j).- Engranaje complementario.
Análogamente al caso de los engranes cónicos de dientes rectos, los engranes cónicos de dentado inclinado sé suponen sustituidos por engranes rectos de dientes inclinados. (Fig. 3.106)
El ángulo de inclinación utilizado es ![]() m
m
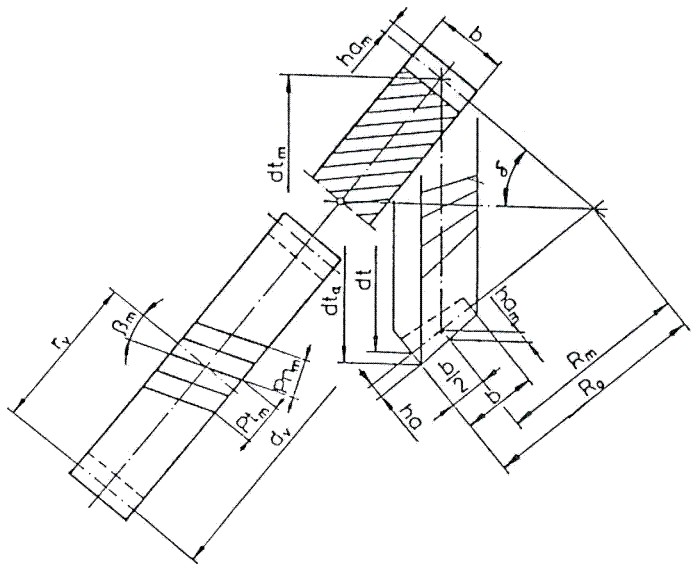
Fig. 3.106 Rueda cónica con dentado inclinado referida a una rueda recta con dentado inclinado.
Relaciones fundamentales.
Numero de dientes equivalentes, de las ruedas frontales complementarias
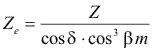 (4.17)
(4.17)Donde:
Z : Numero de dientes del engrane
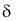 : Angulo primitivo del engrane
: Angulo primitivo del engrane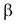 m : Angulo de inclinación en el medio ancho del diente
m : Angulo de inclinación en el medio ancho del dienteDiámetro medio del circulo primitivo (figura anterior)
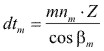
Radio medio de la rueda plana
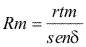
Radio exterior de la rueda plana
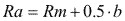
Diámetro del circulo primitivo
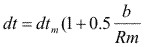
Altura de la cabeza del diente
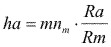
Altura del pie del diente
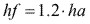
Diámetro exterior
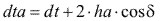
Diámetro interior
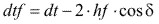
Angulo de la cabeza
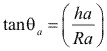
Angulo del pie
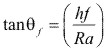
Generalmente, el modulo normal medio mm, se expresa los valores normalizados.
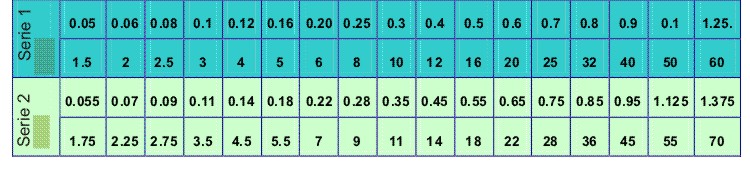
Tabla Series de módulos, en mm, según DIN 780 (Preferentemente se utilizarán los módulos de la serie 1.
Por lo tanto, en el punto medio de la rueda cónica (Fig. 3.106), se tiene una altura de cabezas ham = mnm y una altura de pies hfm = 1.25*mnm.
Relación de contacto.
|
(4.18)
|
Donde:
Paso aparente medio
Numero de dientes imaginario
Modulo aparente
Angulo de presión aparente
Diámetro primitivo de la rueda complementaria media
Distancia imaginaria entre ejes (av)
Diámetro exterior de la rueda media complementaria
Diámetro del circulo base de la rueda media complementaria