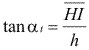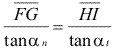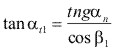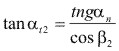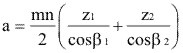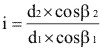3.1.3.- Engranaje Helicoidal.
Engranajes Helicoidales (Recuperado de https://youtu.be/ITxNdwQFEAk)
Una rueda dentada de diente helicoidal puede ser considerada como una superposición de infinitas ruedas dentadas de diente recto, de espesor diferencial, sucesivamente escalonadas. El resultado es la inclinación de cada diente como una hélice cilíndrica a lo largo del cilindro generatriz. Los valores de inclinación de la hélice más utilizados, oscilan entre 10 y 30 grados.
La sección transversal del diente por un plano perpendicular al ángulo de inclinación de la hélice tiene precisamente la misma forma que un perfil de diente recto.

Fig. 3.72
a).- Generalidades.
La disposición inclinada de los dientes, va originar la aparición de esfuerzos tanto en la dirección radial del árbol como en la dirección axial, pudiendo repercutir en la necesidad de montar disposiciones de rodamientos bastante más costosos que los utilizados en los rectos.
Es conveniente, desde el punto de vista del diseño, utilizar disposiciones de engranajes cuya inclinación de dientes sea tal, que se compensen en la medida de lo posible las fuerzas axiales.
Los engranajes helicoidales, tienen los dientes inclinados con respecto al eje (Fig. 3.72).Dicha inclinación viene determinada por el ángulo (![]() ) de la inclinación de la hélice.
) de la inclinación de la hélice.
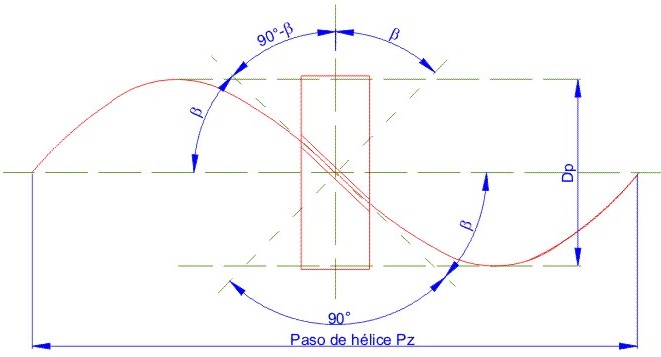
Fig. 3.73 Engranaje helicoidal
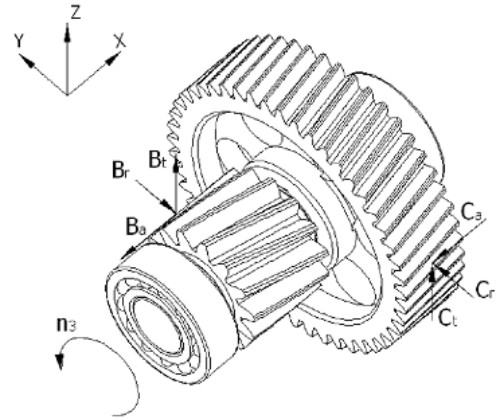
b).- Fuerza en engranajes Cilíndrico-Helicoidales.
En los engranajes cilíndricos de dentado helicoidal, se originan unas fuerzas, que se consideran concentradas en el punto de tangencia de las circunferencias primitivas del piñón y de la corona. Estas fuerzas se producen debido a la forma geométrica del perfil de los dientes (evolvente de círculo), a la transmisión de potencia y velocidad angular producido en el engranaje y a la inclinación del dentado (ángulo de la hélice ![]() ).
).
|
|
Fuerzas axiales (Ba, Ca) no compensadas. Tratar de cambiar el ángulo de inclinación
de los dientes
|
El sentido de las fuerzas axiales que se generan como consecuencia de la inclinación de la hélice, dependen además del giro del engranaje.
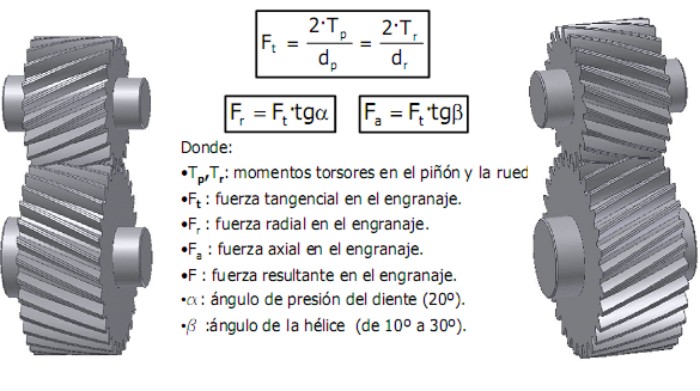
El sentido de las fuerzas axiales que se generan como consecuencia de la inclinación de la hélice, y su sentido depende además del sentido de giro de la rueda conductora.
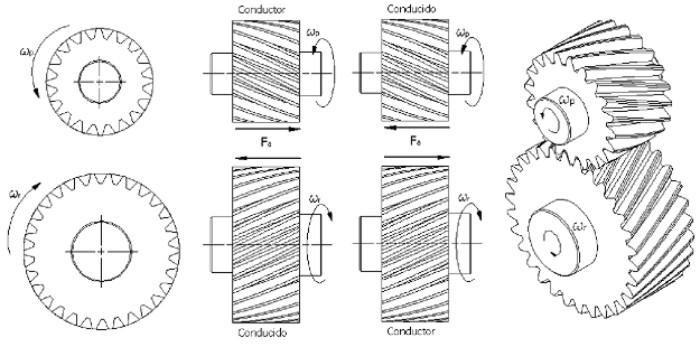
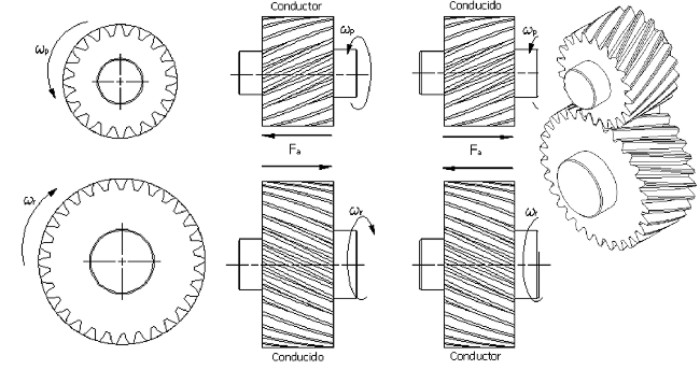
c).- Elementos relacionados con la Helice circular.
Angulo de inclinación de la hélice ![]() : Es el ángulo constante que forma la curva respecto al eje.
: Es el ángulo constante que forma la curva respecto al eje.
Paso de la hélice Pz: Distancia entre dos puntos de la hélice media en el sentido axial.
|
(3.1)
|
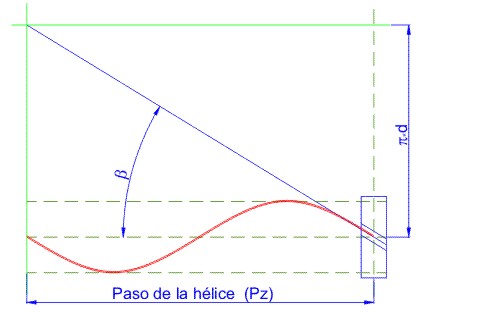
Fig. 3.74 Hélice circular.
Hélice Primitiva - Hélice base.
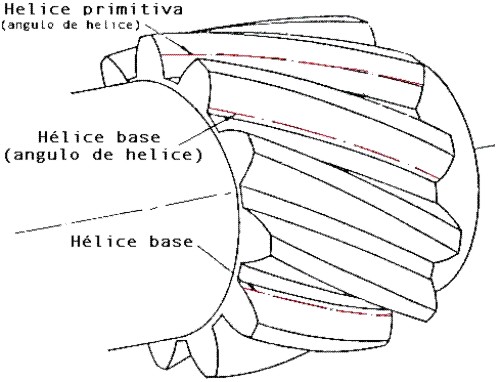
Hélice primitiva: es aquella que esta trazada sobre el cilindro primitivo. (Fig. 3.75 y 3.76)
Hélice base: es aquella que esta trazada sobre el cilindro base. (Fig. 3.75 y 3.76)
Fig. 3.75 Hélice primitiva y hélice base
Fig. 3.76 Engrane helicoidal.
d).- Definición y relaciones fundamentales.
En un dentado helicoidal distinguiremos:
Elementos "circunferenciales o aparentes" (subíndice "t") considerados dentro de todo el plano normal al eje del engrane. (Fig. 3.77)
Elementos "normales" (subíndice "n") considerados dentro de todo plano normal a la hélice primitiva. (Fig. 3.77)
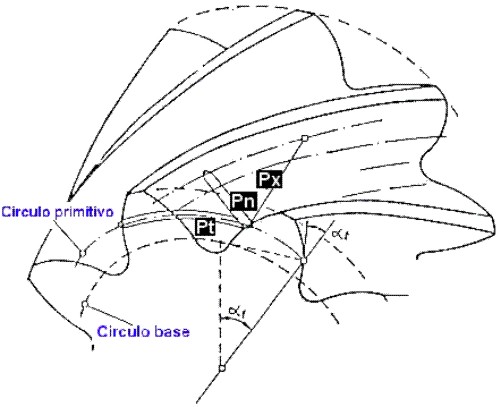
Fig. 3.77 Elementos fundamentales.
Donde:
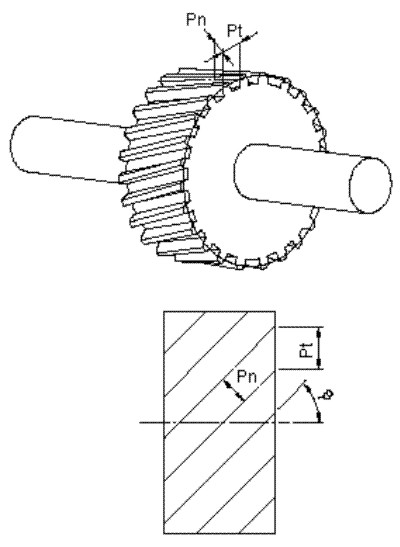
Pt: Paso aparente.- Es la distancia entre dos dientes consecutivos medida sobre el circulo primitivo.
Pn: Paso normal (Fig. 3.78).- Es la distancia entre dos dientes consecutivos medida normalmente a la hélice primitiva sobre el circulo primitivo.
St: Espesor aparente (Fig. 3.78).- (St=Pt/2)
Fig. 3.78 Relaciones fundamentales.
Sn: Espesor normal.- (Sn=Pn/2)
et: Intervalo aparente.- (et=Pt/2)
en: Intervalo normal.- (en=Pn/2)
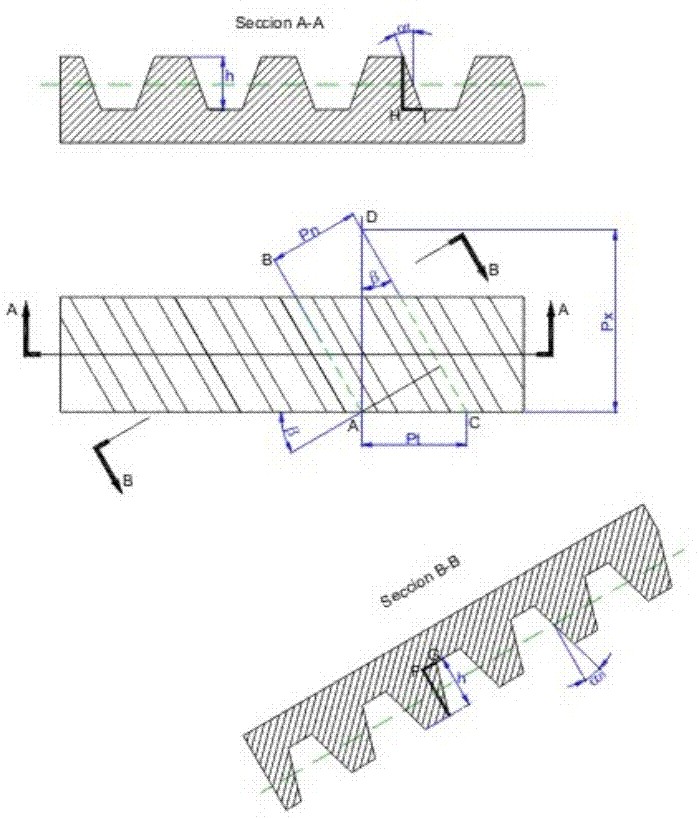
En la Fig.3.79, se representa un engrane helicoidal sobre el cual se ha realizado, un corte por el plano aparente (corte A-A) y otro por el plano normal (corte B-B), con lo cual se definen algunos elementos fundamentales.
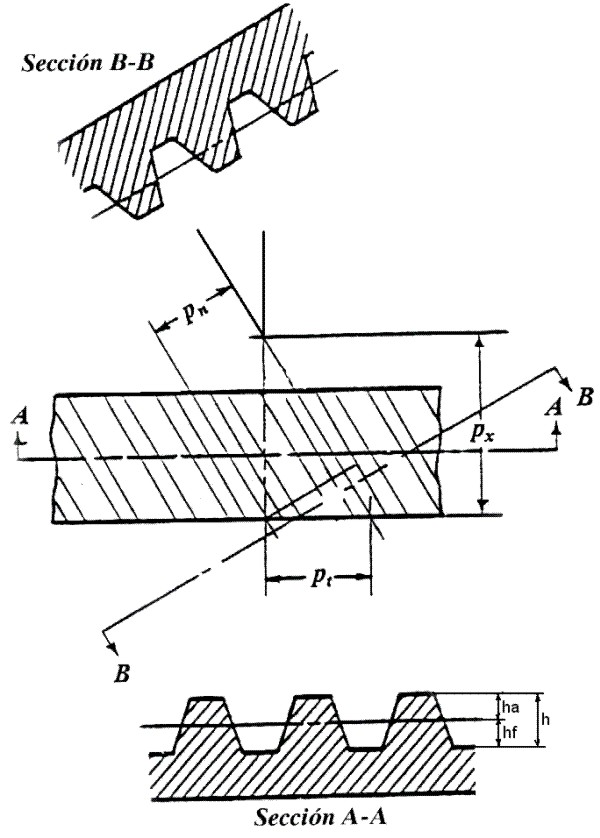
Fig. 3.79 Elementos fundamentales.
Angulo de inclinación de la hélice primitiva (
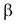 )
)Paso normal.- Pn = mn*
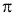 . El modulo normal se elegirá en Tabla (módulos normalizados)
. El modulo normal se elegirá en Tabla (módulos normalizados)Paso aparente.- Pt =mt*
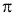 . El módulo aparente se calculará en función del módulo normal (mn) y del ángulo de inclinación de la hélice primitiva (
. El módulo aparente se calculará en función del módulo normal (mn) y del ángulo de inclinación de la hélice primitiva (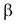 )
)Diámetro primitivo d.
En base a la figura 3.78, la longitud del circulo primitivo es:
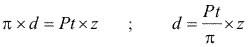 (3.2)
(3.2)Por tanto el diámetro primitivo es: d = mt * Z.
Altura del diente.- h = 2,25 . mn.
Altura de la cabeza del diente (Addendun).- ha = mn.
Altura del pie del diente (Dedendun).- hf = l,25.mn.
Diámetro exterior.- da = (d + 2*mn).
Diámetro del fondo.- df = (d - 2,5*mn).
Angulo de presión normal.-
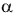 n = 20º
n = 20ºEl dentado'helicoidal es tallado con herramientas de módulo normal, ajustándolas a la pieza con el ángulo de inclinación.
De este modo, el dentado normal con ángulo de presión
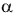 n = 20º, no se forma en el frente del diente, sino en la sección normal situada perpendicular a la línea de los flancos, o sea
n = 20º, no se forma en el frente del diente, sino en la sección normal situada perpendicular a la línea de los flancos, o sea 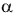 n = 20º.
n = 20º.Angulo de presión aparente
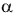 t. Se calculará en función del ángulo de presión normal
t. Se calculará en función del ángulo de presión normal 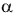 n y del ángulo de inclinación de la hélice primitiva
n y del ángulo de inclinación de la hélice primitiva 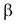
Diámetro base:
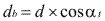
Angulo de inclinación de la hélice base (
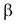 b). Para definir
b). Para definir 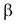 b, se debe considerar que todas las hélices trazadas sobre un mismo dentado, tiene el mismo paso helicoidal. (Pz) (Fig.3.80) de donde:
b, se debe considerar que todas las hélices trazadas sobre un mismo dentado, tiene el mismo paso helicoidal. (Pz) (Fig.3.80) de donde: 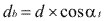
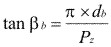
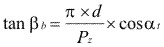
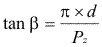
Entonces:
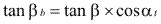 (3.3)
(3.3)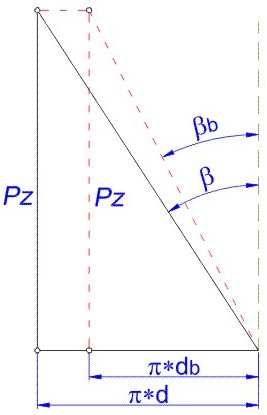
Fig. 3.80 Desarrollo de hélice.
Sentido de la hélice. El sentido de la hélice puede ser a derechas o a izquierdas. (Fig.3.81)
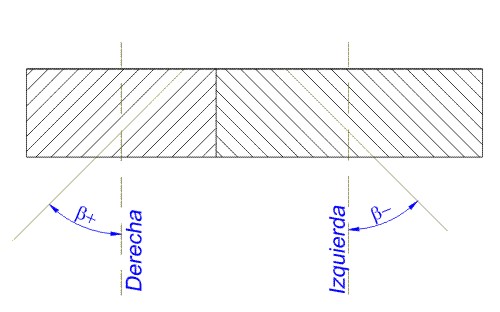
Fig. 3.81 Sentido de la hélice.
e).- Engranaje Piñón - Cremallera.
En la figura 3.82 se ha representado un engranaje Piñón-Cremallera.
Si H1 es la hélice primitiva del piñón de ángulo ![]() , y se hace rodar sin deslizamiento, el cilindro primitivo del piñón sobre el plano primitivo de la cremallera, la hélice primitiva H1 se desarrollara sobre dicho plano según un segmento rectilíneo H2, de ángulo
, y se hace rodar sin deslizamiento, el cilindro primitivo del piñón sobre el plano primitivo de la cremallera, la hélice primitiva H1 se desarrollara sobre dicho plano según un segmento rectilíneo H2, de ángulo ![]() respecto al eje del piñón. Por tanto, los dientes de la cremallera son unos prismas inclinados según el ángulo
respecto al eje del piñón. Por tanto, los dientes de la cremallera son unos prismas inclinados según el ángulo ![]() . El sentido de la inclinación de la cremallera será siempre contrario al sentido de la hélice primitiva del piñón.
. El sentido de la inclinación de la cremallera será siempre contrario al sentido de la hélice primitiva del piñón.
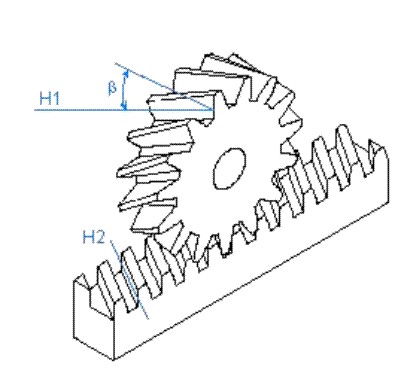
Fig. 3.82 Piñón - cremallera.
Relaciones Fundamentales.
Manteniendo las definiciones anteriores tenemos:
Fig. 3.83 Relaciones fundamentales.
Pt: Paso aparente
Pn: Paso normal
Px: Paso axial
n: Angulo de presión normal
t: Angulo de presión aparente
Según la figura 3.83:
Luego:
Entonces:
Según la figura 3.82 tenemos:
y
Igualando "h" tenemos:
Como:
Entonces:
f).- Engranaje paralelo - Engranaje cruzado.
Anteriormente, se veía que los engranajes helicoidales podían transmitir movimiento entre ejes paralelos y también entre ejes que se cruzan.
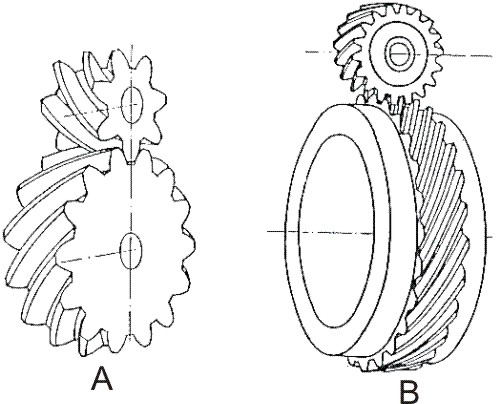
Fig. 3.84
A) Representa un engranaje helicoidal RECTO
B) Representa un engranaje helicoidal CRUZADO.
a).- Características del Engranaje Paralelo.
En la figura 3.85 se han representado los dos cilindros primitivos de un engranaje paralelo, tangentes según la generatriz x-x.
Durante el rodamiento sin deslizamiento de estos cilindros, es primordial que las hélices primitivas conjugadas permanezcan constantemente tangentes.
Esto implica dos condiciones:
Las dos hélices deben ser de sentido opuesto: Una rueda de hélice a derecha solamente puede formar engranaje paralelo con una rueda de hélice a izquierda.
Ambas hélices deben tener el mismo ángulo

Fig. 3.85 Sentido de las hélices.
Desarrollo de las hélices primitivas:
|
(3.6)
|
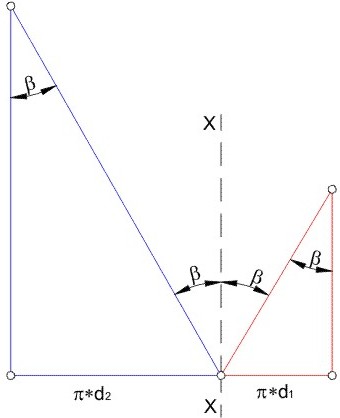
Fig. 3.86 Desarrollo de la hélice.
Distancia entre centros - Relación de transmisión
![]()
|
(3.7)
|
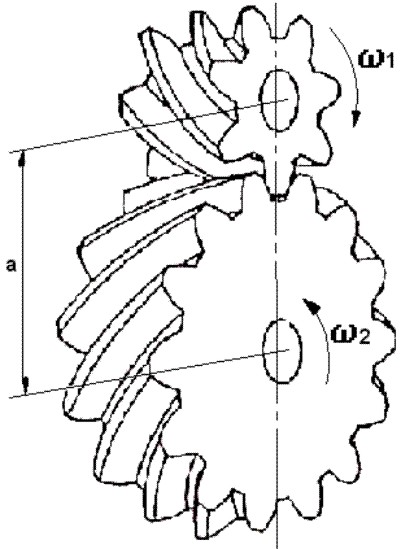
Fig. 3.87 Distancia entre centros.
Características del Engranaje Cruzado.
Para que se realice un engranaje correcto, los dentados conjugados del piñón y de la rueda, han de tener la misma cremallera generatriz. Esto significa que:
Tanto el piñón como en la rueda (![]() n) y (mn) han de tener idéntico valor.
n) y (mn) han de tener idéntico valor.
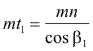
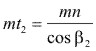
|
(3.8)
|
|
(3.9)
|
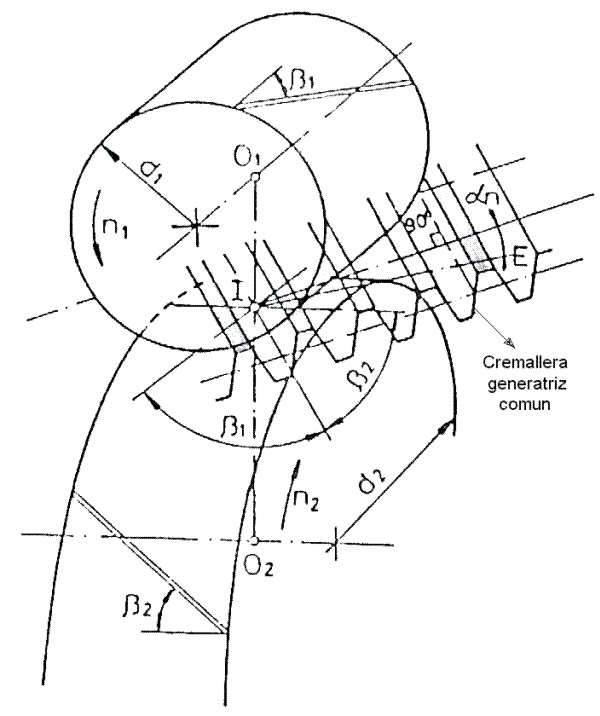
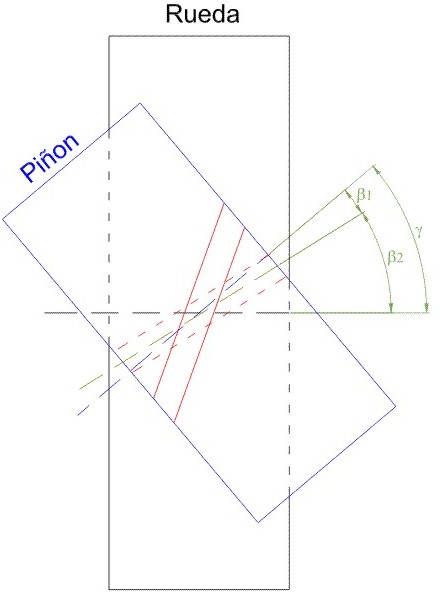
Fig. 3.88 Engranaje cruzado.
Relación entre ángulos de hélice.
= Angulo entre ejes.
= Angulo de la hélice primitiva del piñón.
= Angulo de la hélice primitiva de la rueda.
Hélices de igual sentido:
=
+
Hélices de sentido contrario:
=
-
Fig. 3.89 Relación de ángulos primitivos.
Relación entre ángulos de hélice.
De figura 3.89 se deduce que:
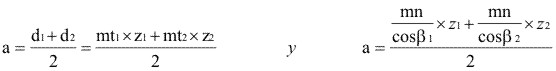
Entonces:
|
(3.11)
|
Si:
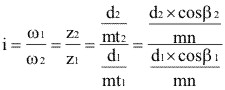
Entonces:
|
(3.12)
|
Distancia entrre centros (a).
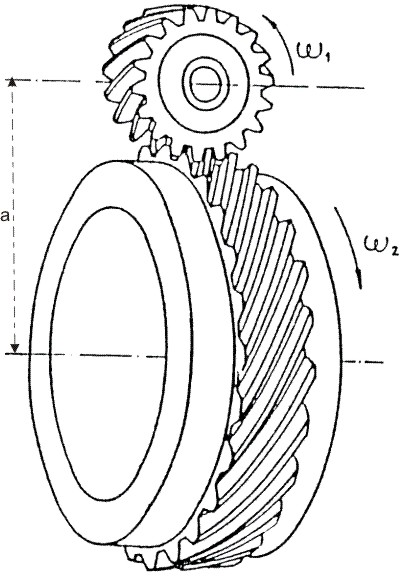
Fig. 3.90 Distancia entre centros.