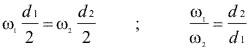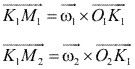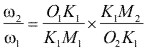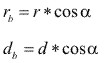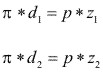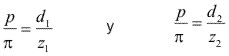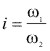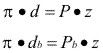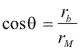Elementos de Máquinas

3.- Elementos de Transmisión Rígidos.

3.1.- Engranajes.

En Video siguiente: Se presenta la geometría de los tipos de engranes usuales en aplicaciones industriales y vehículos en general. También se muestra el concepto de las configuraciones convencionales de ejes paralelos, transmisiones planetarias y transmisiones de tornillo rueda.

Tipos de engranes y transmisiones (Recuperado de https://youtu.be/r8uRa0bZQWw)

3.1.1.- Introducción.

Los engranajes son juegos de ruedas que disponen de unos elementos salientes denominados “dientes”, que encajan entre sí, de manera que unas ruedas (las motrices) arrastran a las otras (las conducidas o arrastradas).

Transmiten el movimiento circular a circular.

La condición para que las ruedas “engranen”, es decir, que puedan acoplarse y transmitir el movimiento correctamente, es que tengan los mismos parámetros o dimensiones en el diente.

Una rueda dentada transmite el movimiento a la contigua que se mueve en sentido opuesto al original.

Sos sistemas muy robustos que permiten transmitir grandes potencias entre ejes próximos, paralelos, perpendiculares o oblicuos, según su diseño. Por el contrario son bastante ruidosos.

Ventajas, inconvenientes y aplicaciones.

Estos mecanismos presentan numerosas ventajas respecto a las correas y poleas, aunque también algunos inconvenientes.

Ventajas:

• Ocupan espacios muy reducidos.
• No tiene posibilidad de deslizamiento.
• Tiene una gran capacidad de transmisión de potencia.
• Podeen un elevado rendimiento.
• Tienen un bajo mantenimiento.

Inconvenientes:

• Son más costosos, más difíciles de fabricar.
• Producen bastante ruído en el proceso de transmisión.

Aplicaciones.

Su uso está muy extendido tanto en máquinas industriales, en automoción, en herramientas; así como también en objetos como electrodomésticos, juguetes,…

Tipos de engranajes.

Video: Tipos de Engranaje.

Según la forma de los dientes

Engranajes rectos	Se utilizan en transmisiones de ejes paralelos. Son uno de los mecanismos más utilizados, y se encuentran en cualquier tipo de máquina: relojes, juguetes, máquinas herramientas, etc.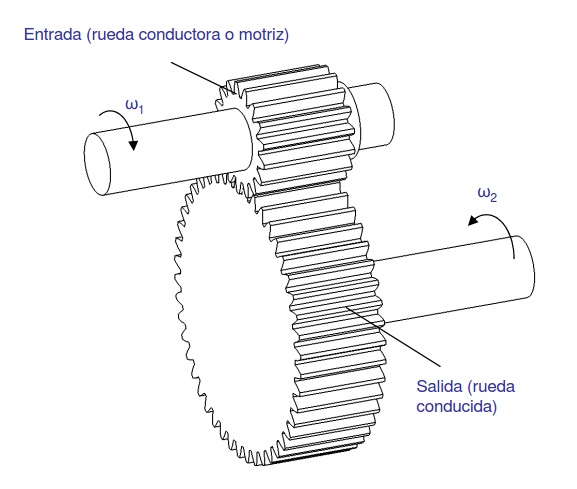
Engranajes Helicoidales.	Sus dientes están dispuestos siguiendo la trayectoria de hélices paralelas alrededor de un cilindro. Pueden transmitir movimiento (potencia) entre ejes paralelos o entre ejes que se cruzan en cualquier dirección (incluso perpendiculares). Este sistema de engrane de los dientes proporciona una marcha más suave que la de los engranajes rectos, ya que en el mismo instante hay varios pares de dientes en contacto, lo cual hace que se trate de un sistema más silencioso, con una transmisión de fuerza y de movimiento más uniforme y segura.
Engranajes Cónicos	Se emplean para transmitir movimiento entre ejes perpendiculares, o para ejes con ángulos distintos a 90 grados. Se trata de ruedas dentadas en forma de tronco de cono, y pueden ser rectos o curvos (hipoides), siendo estos últimos muy utilizados en sistemas de transmisión para automóviles.

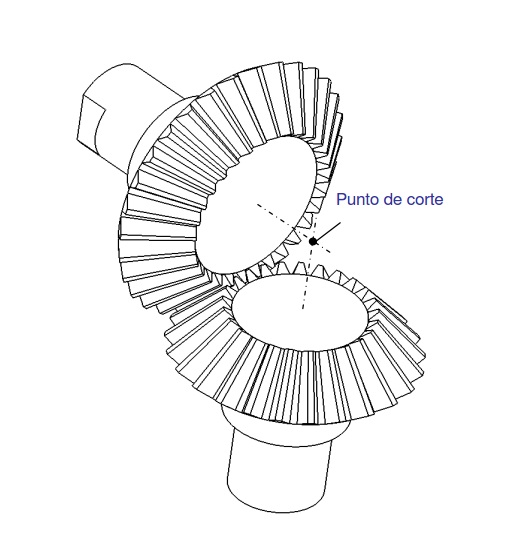 Dibujos extraídos de OCW Cinemática y dinámica de máquinas de la Universidad de Cantabria. Licencia CC-BY-NC-SA.

Según la posición de las ruedas dentadas

Engranajes exteriores	Los dientes de ambas ruedas están tallados en la superficie exterior.
Engranajes interiores	Los dientes de una de las ruedas están tallados en la parte interna.

Imágenes extraídas de: Teoría de máquinas, Universidad Carlos III. Licencia CC-BY-NC-SA.

Según la posición relativa de los ejes

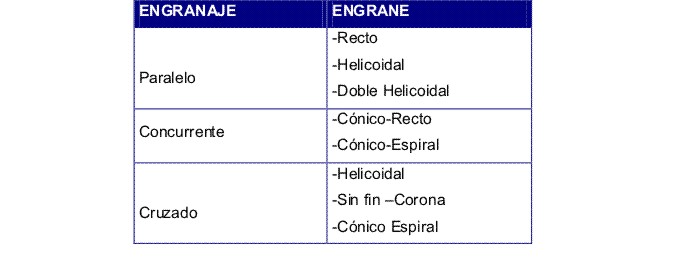
Fig. 3.38

Estos engranajes se consiguen por medio de distintos tipos de engranes que se indican a continuación:

i).- Engranaje paralelo.- Los dos ejes son paralelos.

- De dientes rectos:

Fig. 3.39

Fig. 3.39A Reducción con engranajes cilíndricos de dientes rectos

- De dientes helicoidales:

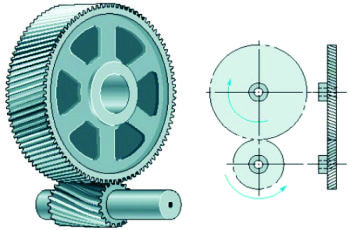
Fig. 3.40a

- De dientes doble helicoidales o V:

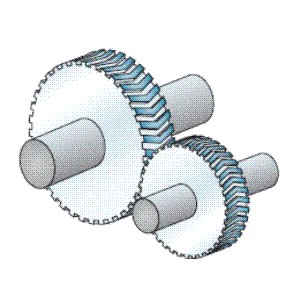
Fig. 3.40b

ii).- Engranajes concurrentes.- Los dos ejes se cortan en sus prolongaciones.

- Engranaje cónico de dientes rectos:

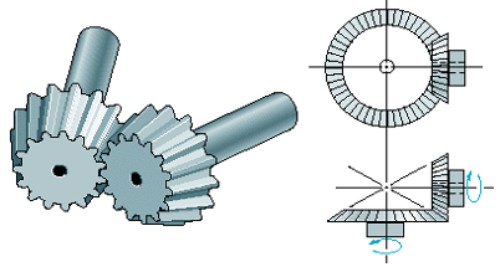
Fig. 3.41

- Engranaje cónico de dientes en espiral:

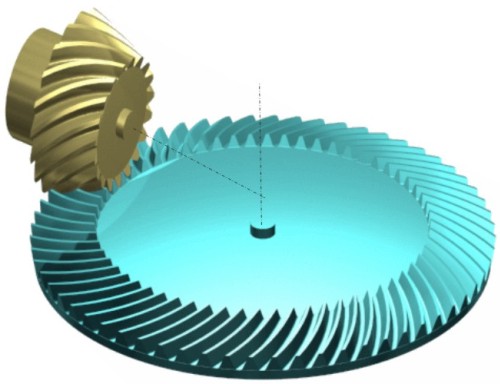
Fig. 3.42

iii).- Engranaje cruzado.- Los dos ejes ocupan una posición relativa cualquiera no son ni paralelos ni concurrentes.

- Engranaje cruzado helicoidal:

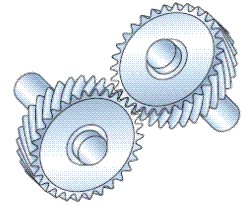
Fig. 3.43a

- Engranaje cruzado cónico espiral o hipoide:

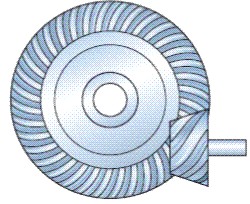
Fig. 3.43b

- Engranaje cruzado Sin fin-corona:

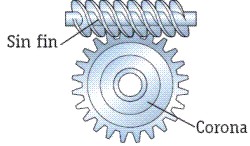
Fig. 3.44

3.1.2.- Engranaje Recto.

RUEDAS DENTADAS - Generalidades y estudio geométrico (Recuperado de https://youtu.be/TSmuQE-hSnw)

a).- Generalidades.

En Video siguiente: Se presentan los aspectos medulares de la geometría de engranes de envolvente (efecto del ángulo de presión y del número de dientes), las proporciones establecidas por la norma AGMA, y las ecuaciones de cálculo de interferencia.

Geometría y cinética de engranes rectos (Recuperado de https://youtu.be/HvCNWlL0qcE)

Los engranes rectos se emplean para transmitir movimientos de rotación entre ejes paralelos o para la transformación de un movimiento de rotación en rectilíneo y viceversa. Su contorno es de forma cilíndrica circular y sus dientes son longitudinalmente paralelos al eje de rotación.

Fig. 3.45 Engranaje recto

Su diseño y forma varia de acuerdo a la aplicación que se le dé. (Fig. 3.46)

Fig. 3.46a Variación de diseños

Las ruedas dentadas pueden ser interiores o exteriores, dando lugar a engranajes exteriores (formados por dos ruedas exteriores) y a engranajes interiores (formados por una rueda exterior y otra interior). Ambos casos pueden observarse en la figura siguiente.

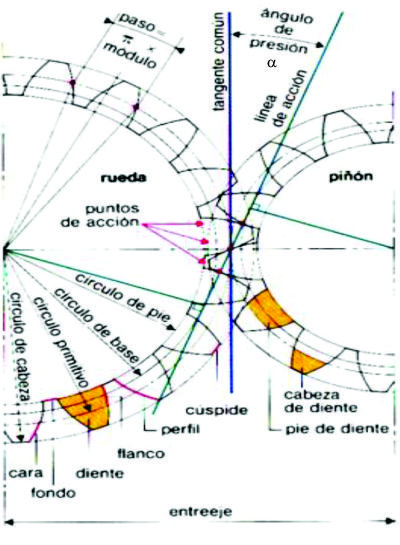
Nomenclatura (lo definiremos con mayor amplitud en Definiciones y relaciones fundamentales).

 

Engranajes Rectos

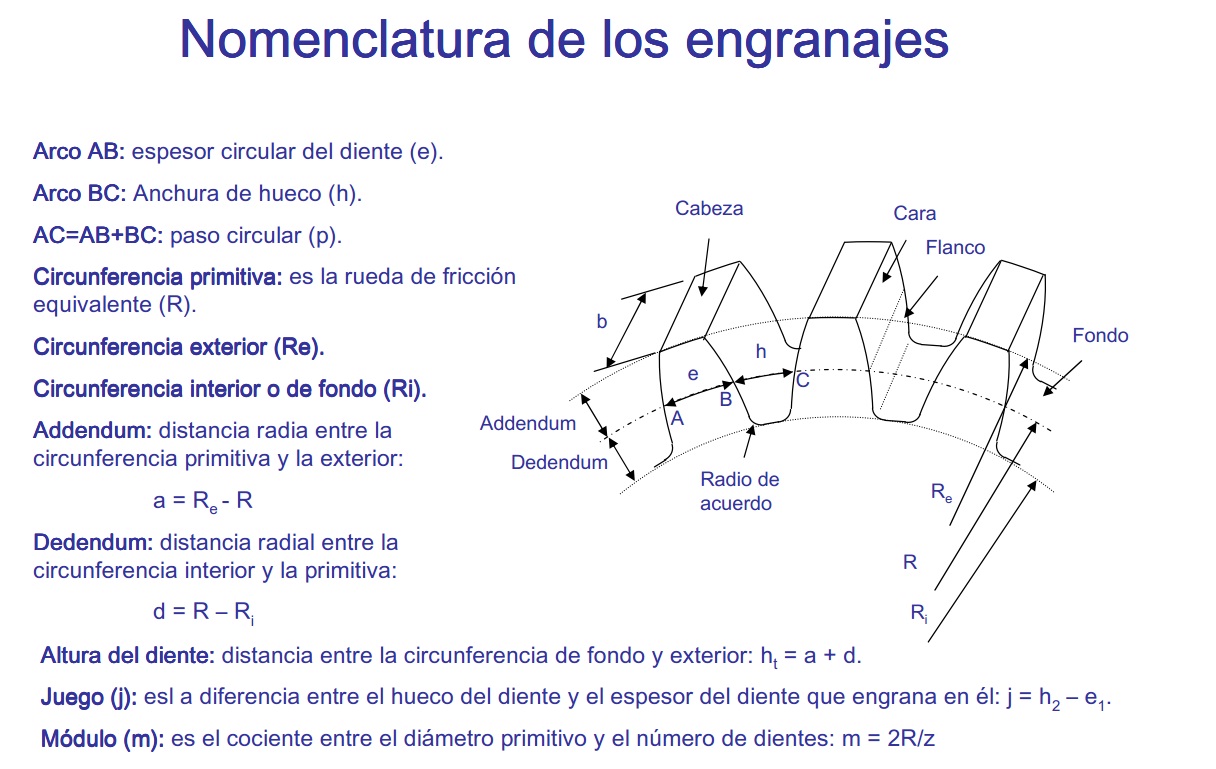
Nomenclatura de los engranajes. En OCW Cinemática y dinámica de máquinas de la Universidad de Cantabria. Licencia CC-BY-NC-SA.

Fig. 3.46b nomenclatura de los engranajes rectos

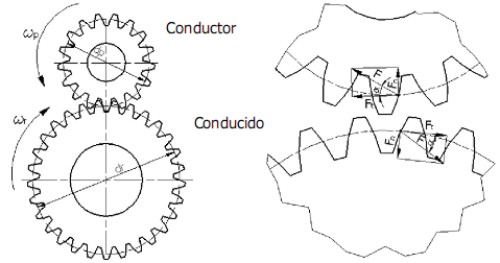
b).- Fuerzas en engranajes Cilíndrico-Rectos. En los engranajes cilíndricos de dentado recto, se originan unas fuerzas, que se consideran concentradas en el punto de tangencia de las circunferencias primitivas del piñón y de la corona. Estas fuerzas se producen debido a la forma geométrica del perfil de los dientes (evolvente de círculo), y a la transmisión de potencia y velocidad angular producido en el engranaje.

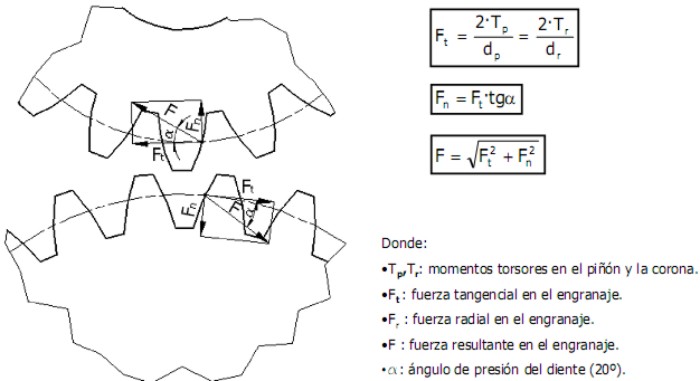
En Video siguiente: Se repasan las ecuaciones de geometría y cinética de engranes rectos fundamentales para su uso con las ecuaciones de la AGMA para cálculo de resistencia. También se propone una aproximación a la resistencia a la fatiga para materiales para los que no se conoce valor AGMA de Sat

Síntesis de ecuaciones de cinética de engranes (Recuperado de https://youtu.be/_LPYi1K0Uf8)

c).- Particularidades de los Engranajes Rectos.

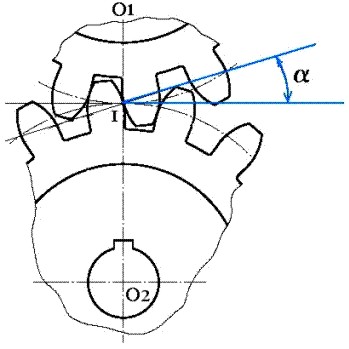
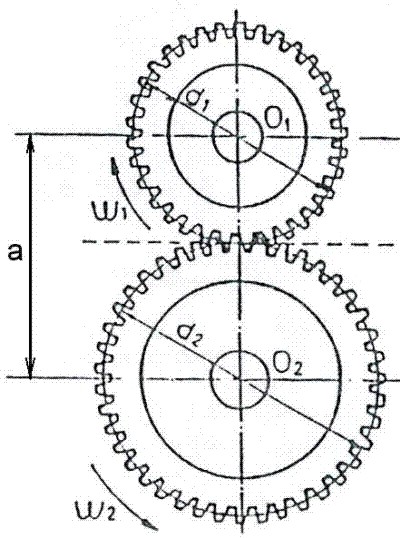
Consideremos dos ejes paralelos O₁ y O₂ (Fig. 3.47) Él eje conductor O₁, gira con una velocidad angular y se desea que el eje conducido O₂, gire en sentido inverso con una velocidad angular .

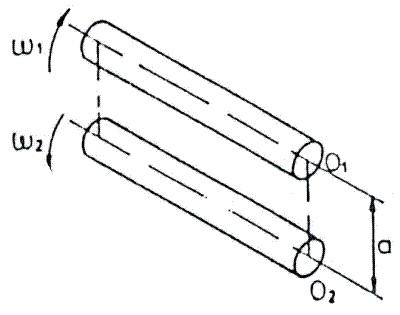
Fig. 3.47 Sentido de giro de 2 ejes paralelos

En este caso se adoptan dos posibles soluciones: Rodillos de fricción o Engranes rectos

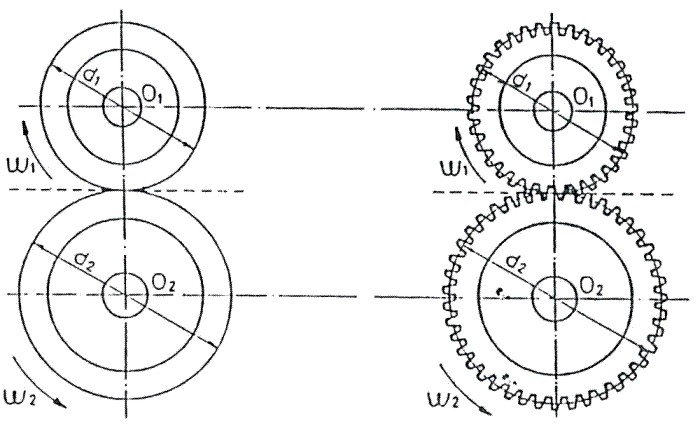
Fig. 3.48 Rodillos de fricción y Engranes rectos

En el caso de los rodillos de fricción, si no existe deslizamiento en el punto de contacto, la velocidad tangencial de ambos rodillos será igual, por tanto:

En el caso de los engranajes rectos, imaginariamente hacen contacto dos circunferencias de diámetros d₁ y d₂, rodando una contra la otra, sin deslizamiento, con lo cual también se cumple:

A estas circunferencias imaginarias de los engranes rectos se les denomina: "Circunferencias primitivas"

Inconvenientes de los rodillos de fricción:

• El arrastre se realiza por rozamiento, por tanto el rendimiento del sistema es bajo.
• En el instante en que los esfuerzos a transmitir sobrepasan ciertos valores, se produce un deslizamiento, con lo cual desaparece el sincronismo entre los dos ejes.

Ventajas de los engranajes rectos:

• El arrastre se realiza por forma, por tanto el rendimiento del sistema es alto.
• Al tratarse de ruedas dentadas, este sistema asegura un sincronismo total entre los dos ejes.

d).- Características del perfil del diente.

Para que los engranajes puedan cumplir su función, es preciso que los perfiles de los dientes cumplan ciertas condiciones, como:

• En todo momento los perfiles han de ser tangentes.
• La relación de velocidades angulares 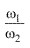debe mantenerse constante en el tiempo. cuando se cumple dichas condiciones se dice que los engranajes tienen ACCION CONJUGADA.

Fig. 3.49

e).- Ley fundamental del engranaje.

RUEDAS DENTADAS - Ley de engrane (Recuperado de https://youtu.be/k2rrAM-h37M)

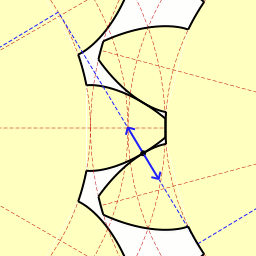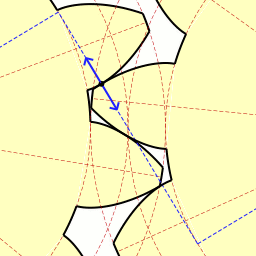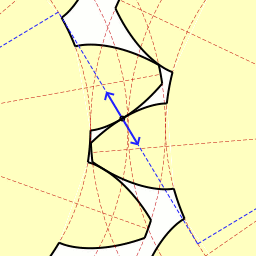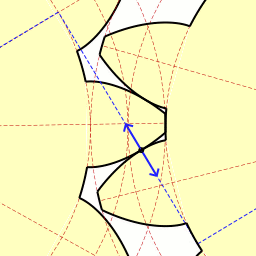
Parámetros a tener en cuenta.

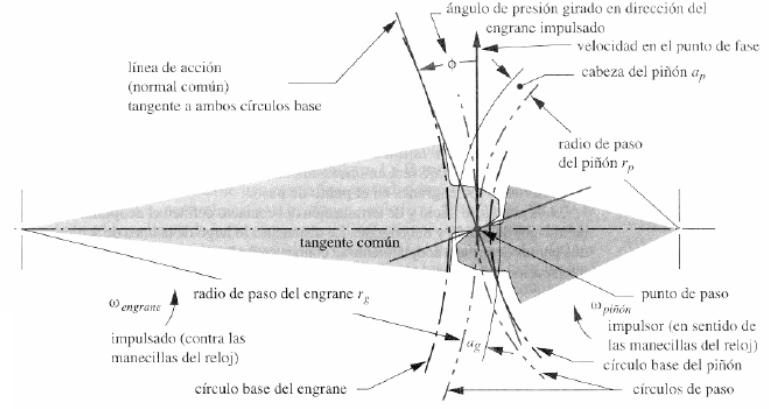
En el análisis que sigue se supone que los dientes están perfectamente formados, y son lisos y absolutamente rígidos.

Para mantener la relación de velocidades angulares constante en el tiempo, el engranaje entre un par de dientes debe ser continuo, desde el punto (A) en el cual se inicia el contacto, hasta el punto(B), donde termina. Ver figura 3.50.

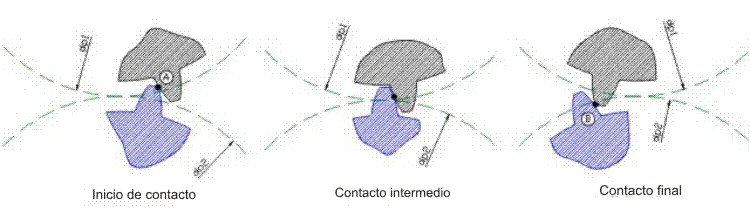
Fig. 3.50 Continuidad del engrane

La recta que se genera desde el punto "A" hasta "B" representa los puntos de contacto sucesivos que se producen durante el engranaje de dos dientes y es la dirección en que actúan las fuerzas.

A esta recta se la denomina: "Línea de acción"

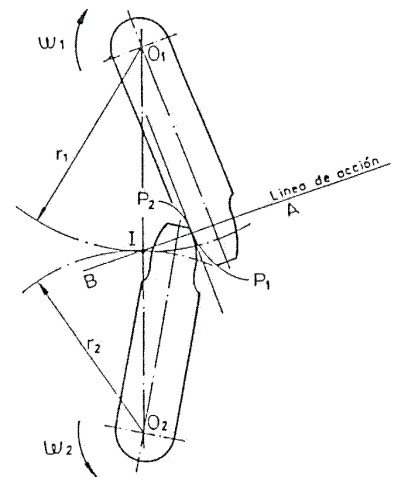
Fig. 3.51 Representación de la línea de acción.

Como se indica en la Fig.3.51 la "línea de acción" corta a la recta que une los centros (O1-O2) en el punto "I", que se denomina:: Punto primitivo

Para una transmisión positiva de movimiento (sin deslizamiento), los dientes no tienen que ser de una forma particular. Sin embargo, para una operación tranquila y sin vibraciones, las velocidades de los círculos primitivos de los dos engranajes deben ser las mismas en todo momento. Este enunciado se refiere especialmente al corto intervalo de tiempo durante el cual dos dientes particulares están en contacto. Si el círculo primitivo del impulsor se está moviendo con velocidad constante, la forma de los dientes debe ser tal que la velocidad del círculo primitivo del engrane impulsado no aumente ni disminuya en ningún instante en que se tocan los dos dientes. Cuando esta condición se satisface, se dice que los engranes cumplen la ley fundamental del engrane.

f).- Ley de velocidades de engrane de los dientes.

En la figura 3.52 se muestran porciones de dos engranes con centros en 0₁ Y O₂, Los engranes tienen velocidades angulares de y , respectivamente.

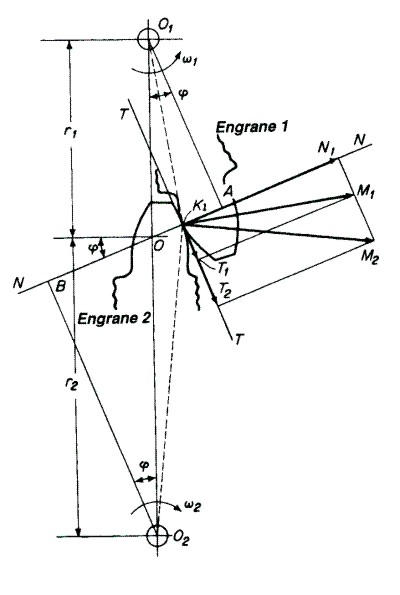
Fig. 3.52 La componente de la velocidad normal a la superficie del diente en un punto de contacto es la misma para ambos engranes.

Los dientes están en contacto en el punto K₁, pero ninguna forma particular se ha especificado aún para el perfil del diente. Las líneas NN y TT representan, respectivamente, la normal y la tangente dibujadas a las superficies del diente en K₁. La normal NN intercepta la línea de centros en el punto O.

El vector K₁M₁ representa la velocidad de K₁ considerado como un punto del engrane 1. El vector es perpendicular al radio 0₁K₁. De manera similar, K₁M₂ representa la velocidad de K₁ cuando K₁ se considera como un punto sobre él engrane 2.

Como los dientes permanecen en contacto, la proyección K₁N₁ de los vectores de velocidad sobre la normal común, debe ser la misma para ambos engranes.

Según la figura,(3.52):

Por lo que:

Por triángulos semejantes, se obtienen las siguientes relaciones:

Sustituyendo en la ecuación (3.82) resulta:

Además, por triángulos semejantes se tiene también:

La sustitución en la ecuación (3.84) da:

La razón debe permanecer constante en todo momento para que no haya cambio en la razón de velocidades de los dos engranes.

Entonces:

También:

El punto 0, es por consiguiente, un punto fijo por el cual se trazan los círculos primitivos. En consecuencia, para satisfacer la ley fundamental del engrane, los lados de los dientes deben estar configurados de modo que la normal trazada por el punto de contacto pase en todo momento por el punto de paso 0.

Puede demostrarse que los dientes de engranes compuestos de involutas o cicloides satisfacen la ley fundamental. Para engranes de involutas, la normal NN no sólo pasa a través del punto O en todo momento, sino que mantiene una inclinación constante con respecto a la tangente común a los círculos primitivos. Para engranes cicloidales, el punto O permanece fijo pero el ángulo varía conforme la posición del punto de contacto K cambia.

Por tanto en el caso de los engranes las componentes normales de las velocidades M₁ y M₂, tienen que ser iguales a N₁

Ó sea:

Entonces:

Así las velocidades lineales de los círculos base de los dos engranajes son también iguales entre sí.

Y la relación de velocidades es:

Ley fundamental del engrane:

"La perpendicular común a los perfiles P₁ y P₂ de los dientes, en todo punto de contacto, debe pasar siempre por un punto fijo (O), de la recta que une los centros de los engranes (O₁ - O₂)"

g).- Perfil de los dientes.

Varias son las formas que pueden satisfacer las exigencias fundamentales de la acción de engranaje, como el perfil de evolvente de circulo y el perfil cicloidal, etc.

La curva que describe este perfil es la que genera el extremo de una cuerda ideal (de espesor cero), inicialmente enrollada en un cilindro, al desenrollarse del cilindro. El perfil de evolvente depende del cilindro utilizado, el cual recibe el nombre de circunferencia de base. La curva y su generación pueden observarse en la siguiente animación.

La curva evolvente posee una propiedad de especial importancia: la cuerda que la genera es siempre normal a la curva. Dicho de otra forma, la normal a la curva evolvente en cualquier punto es precisamente la cuerda enrollada cuando el extremo está en ese punto.

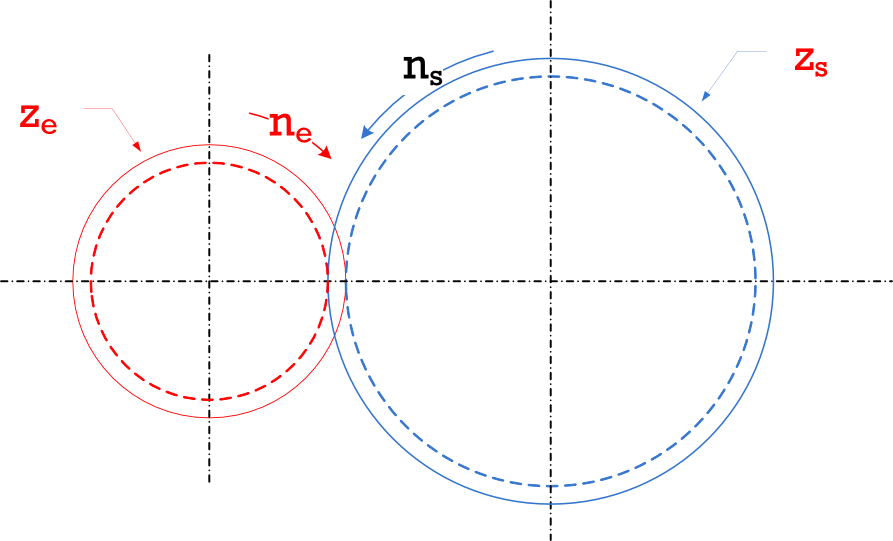
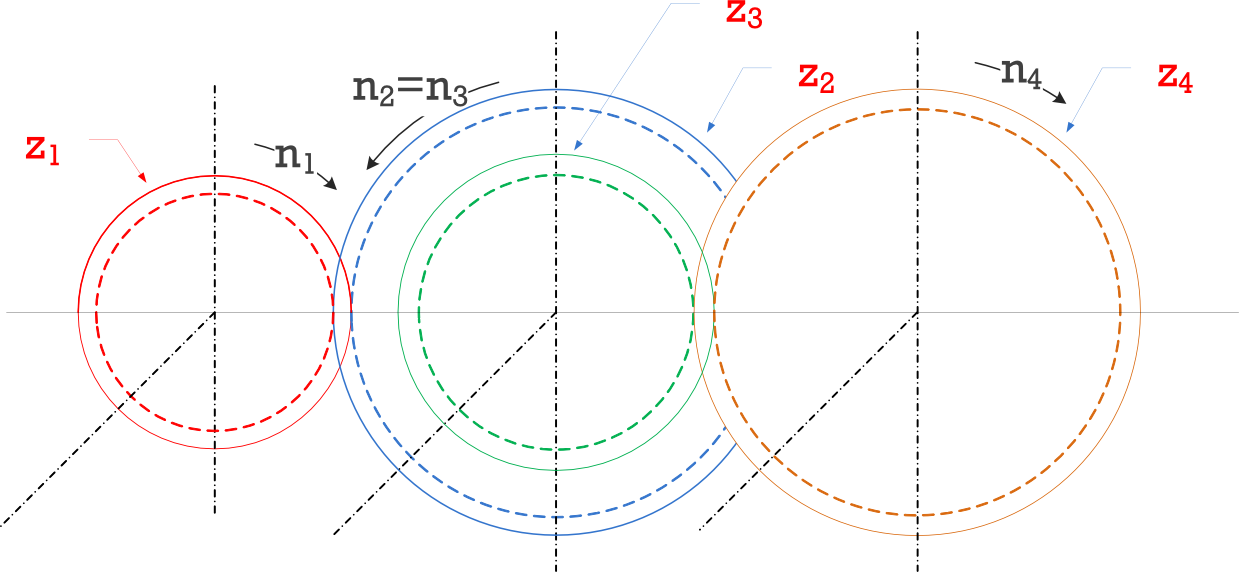
Para comprender cómo se genera el perfil de evolvente entre dos ruedas dentadas que están engranadas, supóngase que se cuenta con dos rodillos y una cuerda enrollada en uno y que llega hasta el otro enrollándose en este último (figura siguiente). Cuando se hace girar uno de los rodillos, este enrolla la cuerda estirando de ella y la cuerda, a su vez, se desenrolla del otro rodillo haciéndolo girar. Si se sigue un punto T de la cuerda se observa que dicho punto sale de un rodillo y si dirige al otro rodillo. Para un observador situado en un sistema fijo Xu-Yu, el punto T traza una recta en su camino desde un rodillo hasta el otro. Sin embargo, para un observador que se mueve con el piñón (es decir, en el sistema Xp-Yp), el punto traza una evolvente (naranja). Y, finalmente, para un observador que se mueve con la rueda (es decir, en el sistema Xr-Yr), el punto traza otra evolvente distinta (azul). En la figura se observa cómo el sistema es cinemáticamente equivalente si se piensa en dos rodillos y una cuerda que si se piensa en los dos perfiles de evolvente que se empujan uno a otro. La relación de velocidades angulares es constante en todo momento. Además, también se observa que en el contacto entre los dos perfiles de evolvente existe, a veces, un gran deslizamiento.

Si el perfil de evolvente utilizado fuera tan largo como se muestra en la figura anterior, los dientes de una rueda chocarían con la otra rueda. Por este motivo, en la práctica se emplea un tramo más corto del perfil de evolvente. Aun así, se puede observar cómo el contacto sigue igualmente la recta tangente a las circunferencias de base. Entre dos dientes, el contacto desaparece cuando se termina el tramo del perfil de evolvente, aunque en ese instante ya hay otro contacto que asegura la continuidad del movimiento (ver animación de Fuerzas en engranajes Cilíndrico-Rectos).

Pero en este estudio solamente se va a considerar el perfil de: Evolvente de círculo

Las ventajas del sistema de engranajes con perfil evolvente son las siguientes:

• Economía del procedimiento de tallado. Número de útiles reducido.
• Curva continua en todo el flanco (recta en la cremallera). En el sistema cicloidal, el flanco está formado por dos curvas, y por tanto, la ventaja del primero, en cuanto a facilidad de mecanizado, es indudable.
• Los engranajes con dientes en evolvente, son los únicos que pueden funcionar con distancias entre centros variables conservando la relación de velocidades angulares.
• El diente con perfil de evolvente es más sólido a igualdad de paso, que el cicloidal.

h).- Dentado envolvente.

La curva está descrita por un punto de una línea, cuando ésta rueda sin deslizar sobre una circunferencia (Fig. 3.53). También se puede definir como la curva trazada por el extremo de una cuerda inextensible, que se mantiene tirante, mientras se desenrolla de un cilindro llamado: Cilindro base

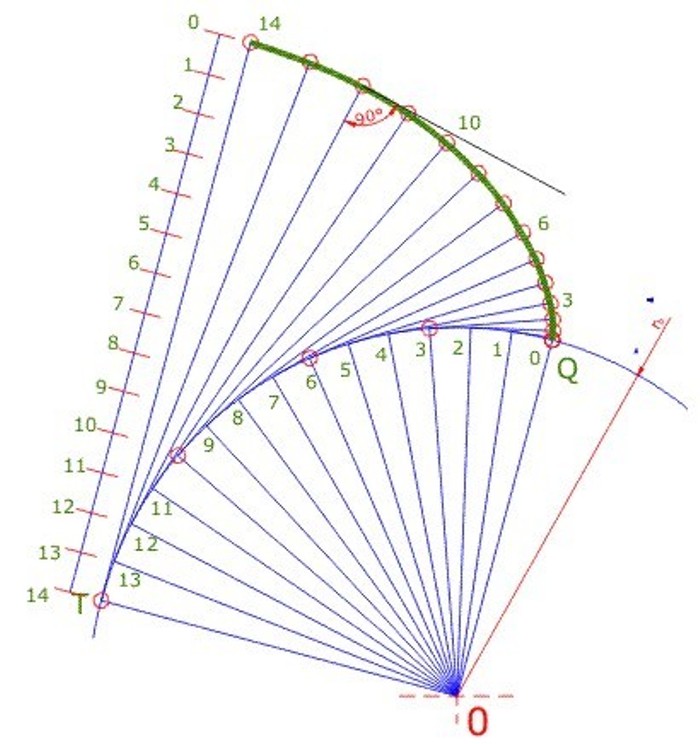
Fig. 3.53 Perfil de evolvente.

i).- Propiedad de la envolvente.

• Considerando la cuerda tensada (TV) tangente al circulo y arrollándosela a dicho circulo, hasta el punto Q, se deduce:

  TQ = TV

• El Centro instantáneo de rotación de la cuerda (TV), está siempre situado en su punto de tangencia con la circunferencia base.

• La perpendicular a la evolvente en cualquier punto, es tangente a la circunferencia base.

A continuación se presenta otro sistema, con el cual es posible desarrollar un perfil de evolvente (Fig.3.54)

A medida que se desplaza la cuerda hacia la izquierda (b) (manteniéndola siempre tirante), el cilindro gira, con lo cual el punto va trazando sobre la brida (E) el perfil de evolvente como se indica en (c).

Él circulo sobre el cual se genera el perfil de evolvente se define como: Circulo base

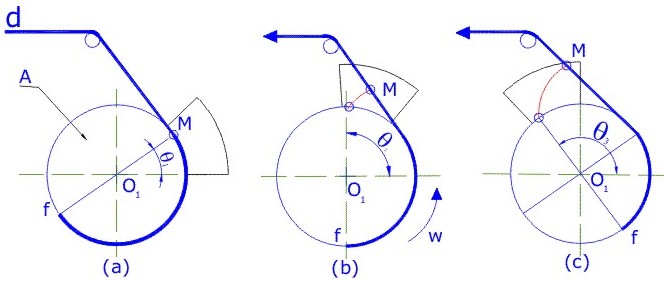
Fig. 3.54 Desarrollo del perfil de evolvente.

j).- Características geométricas.

*).- Perfiles conjugados.

En el apartado anterior se decían las condiciones que han de satisfacer los perfiles conjugados. A continuación se presenta un sistema con el cual es posible desarrollar los perfiles conjugados de los dientes, en evolvente.

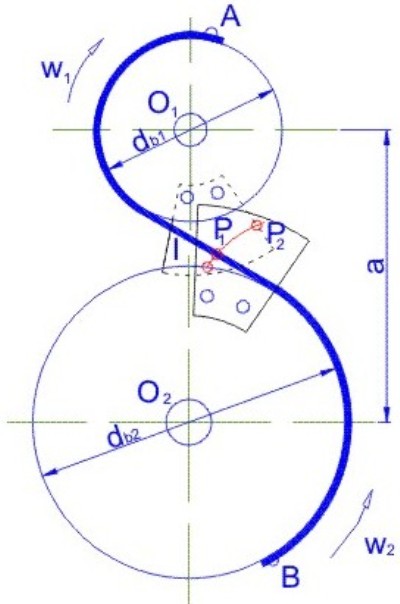
En la (Fig. 3.55), se indican los cilindros base de cada engrane, con centros 0₁ y 0₂.

Se enrolla una cuerda (A-B) sobre los cilindros, con un punto trazador montado en M, que está en contacto con las bridas montadas sobre los dos cilindros.

A medida que el cilindro superior gira (), la cuerda se desplaza y hace girar al cilindro inferior (), con lo cual el punto trazador describe los dos perfiles de evolvente P₁, P₂ sobre las bridas correspondientes a los cilindros base de diámetro d_b1 y d_b2.

Fig. 3.55 Perfiles conjugados.

La cuerda, que es tangente a ambos cilindros base, es la perpendicular común a los perfiles conjugados P₁, P₂ en el punto de contacto M, puesto que una tangente a los cilindros base es siempre perpendicular a la evolvente correspondiente. Esta cuerda, corta a la recta que une los centros O₁ y O₂ en el punto fijo "I" (punto primitivo) y así queda satisfecha la ley fundamental del engranaje.

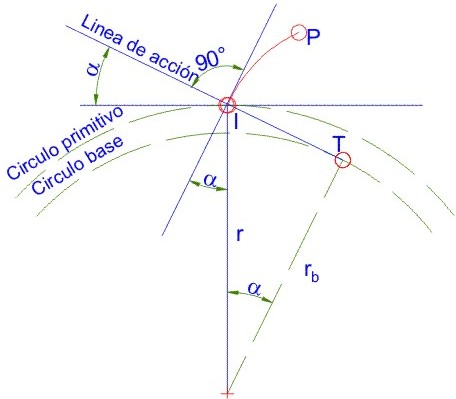
**).- Ángulo de presión ()

Fig. 3.56 Ángulo de presión.

Se llama ángulo de presión () al ángulo formado por la línea de acción y la perpendicular a la recta que une los centros O1-O2 (Fig. 3.56)

***).- Relación entre diámetro base y diámetro primitivo.

Fig. 3.57 Diámetro base y diámetro primitivo.

De la figura 3.64, utilizando las relaciones del triangulo se deduce:

(3.92)

4*).- Paso Primitivo - Módulo (m).

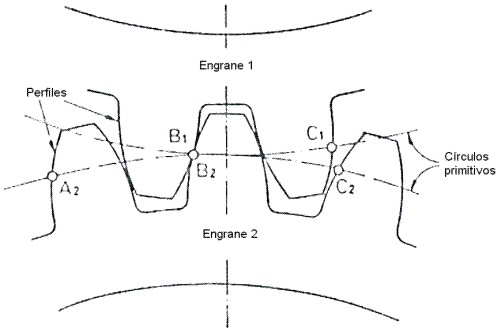
En la (Fig. 3.58), se han trazado las dos circunferencias primitivas y algunos dientes sucesivos de dos engranes. Los dientes están evidentemente espaciados de forma regula sobre los círculos primitivos correspondientes.

Fig. 3.58 Engranaje entre dientes.

Paso primitivo (P): es la distancia entre dos perfile homólogos consecutivos, medida sobre el círculo primitivo.

Para realizar el engranaje, el paso de ambos engrane debe ser el mismo.

Siendo Z₁ y Z₂ los números de dientes de los engranes la longitud de los círculos primitivos es:

De donde:

(3.93)

Al termino, () se le denomina modulo (m)

(3.94)

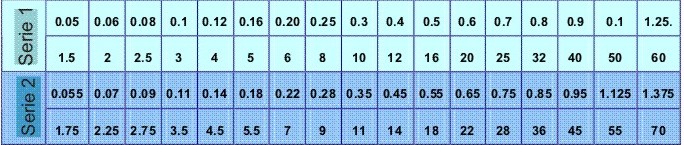
En la tabla 3.1, se presentan los módulos normalizados.

Tabla 3.1. Series de módulos, en mm, según DIN 780
(Preferentemente se utilizarán los módulos de la serie 1.)

Distancia entre centros - relación de transmisión

En un engranaje Fig.3.59, generalmente las condiciones de partida son:

• Distancia entre ejes "a", (llamado distancia entre ejes a la semi-suma de los diámetros primitivos de los engranes).

• Relación de transmisión "i", (llamado relación de transmisión a la relación de velocidades angulares correspondientes a los engranes.

  

Fig. 3.59 Distancia entre centros.

Donde:

(3.94)

5*).- Paso base.

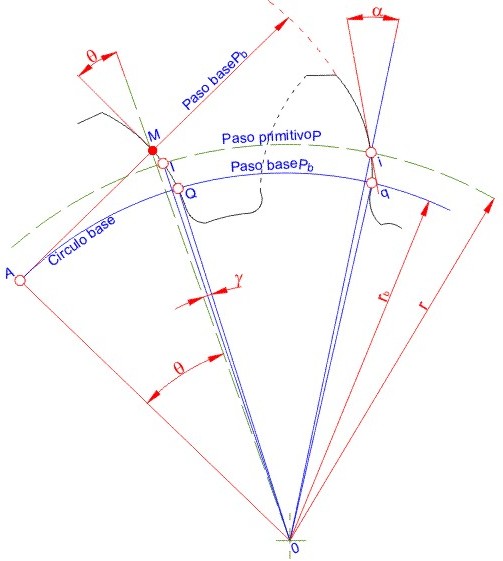
Paso base es la distancia entre dos perfiles homólogos consecutivos medida sobre una perpendicular común a los dos perfiles o sea una tangente cualquiera al circulo base (Fig. 3.60). También se define como la distancia entre dos perfiles homólogos medida sobre él circulo base.

Fig. 3.60 Paso base

Siendo z, el numero de dientes del engrane, la longitud del circulo base es:

Y la relación del paso primitivo y paso base es:

Igualando las dos expresiones:

y;

(3.95)

6*).- Ángulo de imcidencia ().

El ángulo de incidencia (Fig. 3.60) es el ángulo que se forma, en un punto cualquiera "M" de la envolvente, la tangente a la curva con el radio coincidente en este punto (r_M = radio del circulo que pasa por M).

El ángulo de presión es el ángulo de incidencia sobre él circulo primitivo.

(3.96)

(3.97)

7*).- Función "envolvente".

Vamos a situarnos en un punto "M" cualquiera de la envolvente Fig.3.60 donde el ángulo de incidencia es "". Sea el punto donde dicha envolvente encuentra el circulo-base. Se demuestra que:

(paso base)

de donde según la Fig. 3.60 el ; expresado en radianes.

y la función () es la que se llama:

Existen tablas de función envolvente facilitando los cálculos muy numerosos que utilizan esta función.

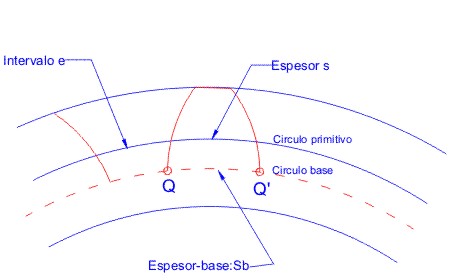
8*).- Espesor (S) - Intervalo (e).

Para un dentando normal y sin juego entre flancos se debe cumplir:

Tenemos para los dos órganos de engranaje:

y para un engranaje sin juego resulta además:

por tanto:

Espesor- base: s_b

Es necesario considerar aquí los puntos donde las envolventes encuentran al circulo -base

Fig. 3.61 Diente de un engranaje recto.

k).- Definiciones y relaciones fundamentales.

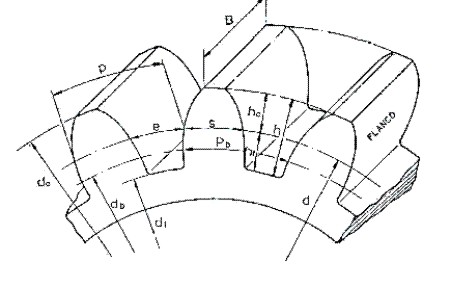
Fig. 3.62 Elementos de un engranaje.

Diámetro exterior.- Es el diámetro correspondiente a la circunferencia que limita el diente exteriormente.

Diámetro del fondo.- Es el diámetro correspondiente a la circunferencia que limita el diente interiormente.

Altura del diente.- Es la distancia radial comprendida entre las circunferencias exterior y del fondo.

Altura de la cabeza del diente (add).- Es la distancia radial entre las circunferencias exterior y primitiva.

Altura del pie del diente (ded).- Es la distancia radial entre las circunferencias primitiva y del fondo.

Proporciones del dentado normal

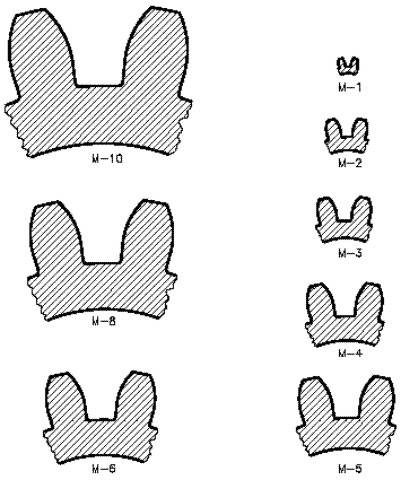
Fig. 3.63

l).- Ruedas de dentado interior.

El engranaje interior generalmente se utiliza cuando existe el problema de espacio (Fig.3.69)

Fig. 3.64

m).- Engranaje Piñón Cremallera.

El engranaje piñón cremallera es un sistema que permite transformar un movimiento de rotación en rectilíneo y viceversa

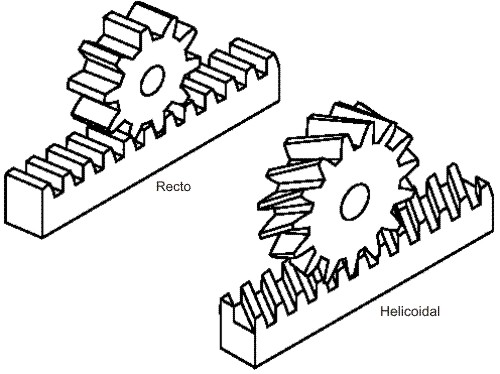
Fig. 3.65 Piñón cremallera (dientes perpendiculares y dientes inclinados)

La cremallera puede concebirse, como un engrane con un circulo primitivo infinitamente grande, tan grande que la línea primitiva es una recta.

Para los dentados en envolvente, el circulo base correspondiente, es también infinitamente grande y con ella, igualmente, el radio de curvatura de los flancos, de manera que éstos son rectos. (Fig.3.66)

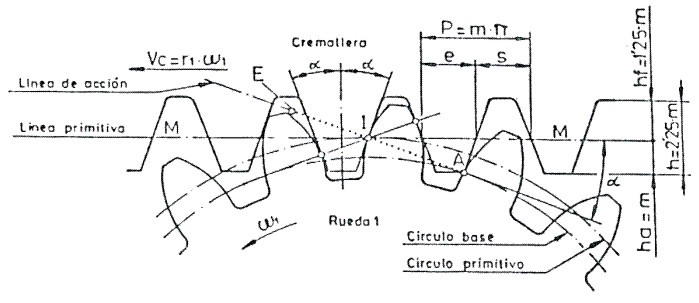
Fig. 3.66 Relaciones fundamentales.