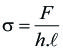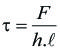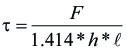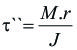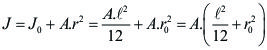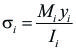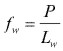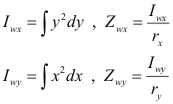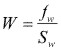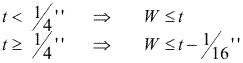1.3.- CÁLCULO DE ESPESOR DE SOLDADURA.
Se entiende que para las juntas soldadas se ha elegido el material de aporte adecuado al material base y en lo que respecta al cálculo, es recomendable que la resistencia del material de aporte sea en lo posible mayor que del metal base, por lo que se espera en caso de fallas, éstas se produzcan en la zona adyacente al cordón.
Bajo esta consideración, los cálculos se ceñirán básicamente a cordones de soldadura de filete y en cordones a tope con penetración parcial en caso de requerir su resistencia.
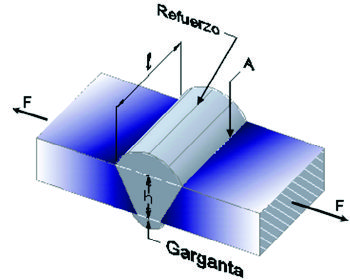
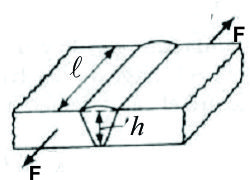
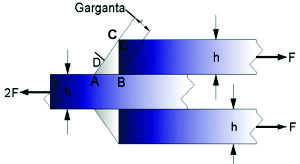
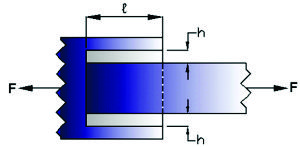
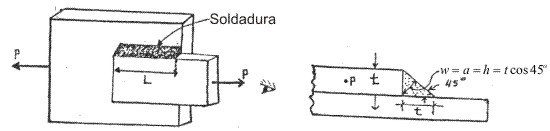
En el caso de una unión de dos planchas como en el caso mostrado en la figura 1.3 se establecen dos hipótesis básicas:
Las planchas permanecen separadas después de construído el cordón de soldadura. Como en el caso de una unión apernada, donde la interracción entre las planchas a unir está asegurada por la acción de los pernos que siempre las mantienen apretadas entre sí, en el caso de planchas soldadas en la mayoría de los casos las planchas pueden quedar levemente separadas, por lo que los esfuerzos sólo los absorbe el cordón de soldadura.
Se supone para el cálculo de esfuerzos teóricos en el cordón de soldadura, las planchas a unir son rígidas. Cualquier cálculo que considere la elasticidad de las planchas a unir deberá hacerse en forma numérica, por ejemplo con programas por elementos finitos.
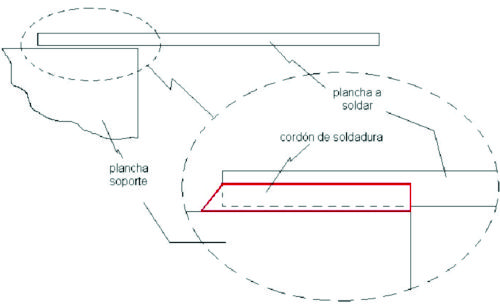
Fig. 1.3
Cuando la acción de fuerzas y/o momentos producen distintos efectos sobre el cordón de soldadura, existen métodos para cuantificar los efectos en forma individual a cada acción.
1.3.1.- Uniones con soldadura a tope.
|
En la figura 1.3.1 puede verse una soldadura sencilla con el surco en V, sometida a la tracción F. Para la carga de tracción o compresión, la tensión normal media es:
En donde h es la garganta de la soldadura y Si existen las cargas de fatiga, es buena práctica el eliminar por mecanizado o rectificado dicho efuerzos.
La tensión media en una soldadura a tope debida a la carga de cizalladura o corte es:
|
Fig. 1.3.1. Unión a tope en tensión.
Fig. 1.3.2. Unión a tope en cizalladura o cortante. |
La soldadura a tope no debe producir discontinuidad en la sección y su sobre-espesor no será mayor que el 10% del espesor de la chapa más delgada; si las chapas son de distinta sección, la de mayor sección se adelgazará en la zona de contacto con pendientes no mayores que el 25% para obtener una transición suave de sección.
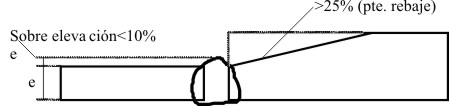
Fig. 1.3.3
Las normas dicen que una soldadura a tope que una totalmente dos piezas realizadas con las condiciones recogidas en las normas y cuyo espesor no sea menor que el espesor de la pieza mas delgada, no requiere cálculo.
1.3.2.- Soldaduras en ángulo o de filete.
|
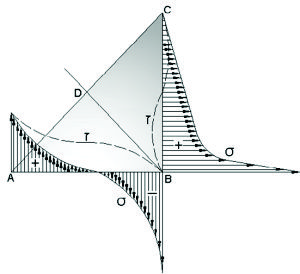
La distribución de las tensiones en las soldaduras en ángulo se ha investigado por procedimientos fotoelásticos, pero los intentos de resolver el problema por los métodos de la teoría de la elasticidad no han tenido apenas éxito. El modelo de la soldadura transversal en ángulo de la figura 1.3.4 se construye fácilmente para ensayos fotoelásticos y tiene la ventaja de una condición de carga equilibrada. Norris construyó este modelo y anotó la distribución de tensiones a lo largo de las caras AB y BC de la soldadura. Un gráfico aproximado de los resultados que obtuvo se muestra en la figura 1.3.5. Obsérvese que existe concentración de tensiones en A y B, en la cara horizontal, y en B en la vertical. Norris indicó que no podía determinar las tensiones en A y B con certidumbre. |
Fig. 1.3.4. Soldadura de filete transversal. |
|
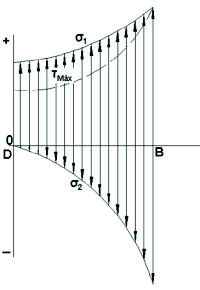
Salakian ha presentado datos de la distribución de tensiones a través de la garganta de la soldadura (fig. 1.3.6). Este gráfico es de interés particular, porque los proyectistas y analistas de tensiones suponen normalmente que el fallo se verifica en la garganta al determinar la resistencia de una soldadura. De nuevo, la figura muestra concentración de tensiones en el punto B. Obsérvese que la figura 1.3.5 se aplica al metal de la soldadura o al metal matriz. La figura 1.3.6, naturalmente, da la distribución de tensiones solo en la soldadura. |
Fig. 1.3.5. Diatribución aproximada de tensiones sobre las caras de la soldadura de filete de la figura 1.3.3, según Norris. |
|
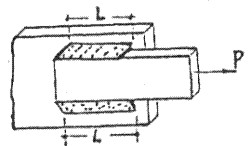
No existe ningún método analítico de obtener las tensiones a partir de estas dos figuras. Por consiguiente utilizaremos los métodos desarrollados en esta pagina, es decir, dimensionando las secciones rectas a las áreas, de modo que resulten unas tensiones nominales o medias satisfactorias y, cuando las uniones están sometidas a cargas de fatiga, por aplicación de los coeficientes de reducción de resistencia, por fatiga Kf a la resistencia del metal de soldadura o de los elementos matrices, según para qué conjunto se hayan hecho los cálculos. La unión a solape sometida a tracción de la figura 1.3.7 tiene un área de garganta de 0.707h |
Fig. 1.3.6. Diatribución aproximada de tensiones principales y de la tensión máxima de corte a lo largo de la garganta de una soldadura de filete, según Salakian. |
La tensión media es entonces:
|
[3]
|
|
Nótese especialmente que las palabras “tensión media” significan que hemos supuesto que esta tensión está uniformemente distribuida en el área total. Además, puesto que ésta es la tensión empleada para dimensionar la soldadura, el empleo de esta ecuación implica que se ha supuesto que todas las tensiones normales en la garganta son cero. Esto está lejos de ser cierto, como se evidencia por los resultados experimentales de la figura 1.3.6. Sin embargo, si la ecuación se emplea con las tensiones máximas permitidas por las diversas normas de construcción, las soldaduras resultantes son perfectamente seguras. No obstante, pueden obtenerse economías, si se estudian otras aproximaciones racionales. |
Fig. 1.3.7. Unión a solapa de doble filete. |
|
En el caso de soldaduras de filete paralelas (fig. 1.3.8), la suposición de una tensión de corte a lo largo de la garganta es más real. Puesto que hay dos soldaduras, el área de la garganta para ambas es A=(2)(0,707h |
Fig. 1.3.8. Soldadura de filetes paralelos. |
|
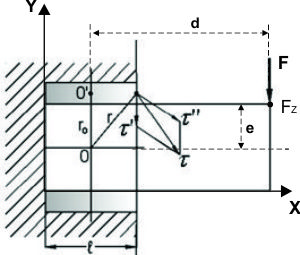
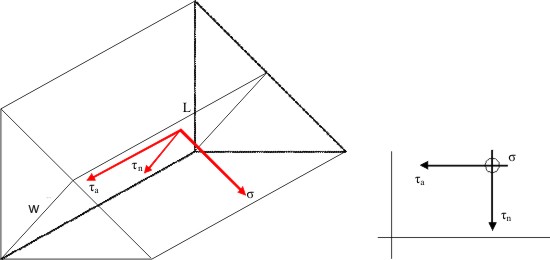
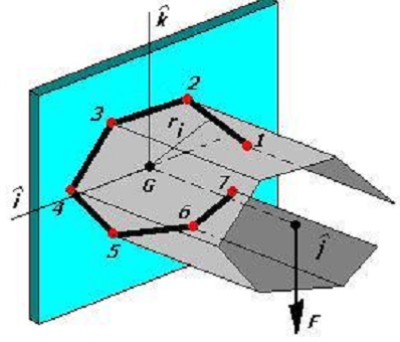
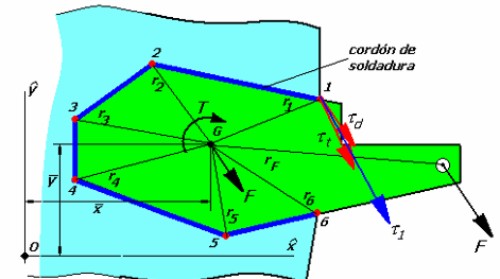
Un tipo de conexión soldada que se encuentra con mucha frecuencia en el proyecto de máquinas es el que se ilustra en el voladizo de la figura 1.3.9. Las reacciones en el soporte son un esfuerzo cortante V y un momento torsor M, que está dado por la relación Fxd donde la distancia d corresponde a la distancia entre la línea de acción de la fuerza que produce la torsión y el centroide O. El centroide O de los cordones representa el punto por donde pasa hipotéticamente el eje polar respecto al cual se produce la torsión. El efecto de estas reacciones es el de producir tensiones de corte primarias y secundarias en las soldaduras. Estas tensiones deben sumarse vectorialmente, como en las conexiones remachadas cargadas excéntricamente, con objeto de obtener la tensión resultante que actúa sobre cada soldadura. Las tensiones primarias se obtienen como se describirá posteriormente. La tensión secundaria se obtiene independientemente para cada soldadura del grupo. Sea el punto O en la figura 1.3.9 el centro de gravedad del grupo con r como el radio de cualquier punto de una de las soldaduras. |
Fig. 1.3.9. Conexión con Momento. |
La tensión secundaria se obtiene de la fórmula de la torsión y puede escribirse:
|
[4]
|
En la que J es el momento polar de inercia de la soldadurarespecto al punto O. La tensión máxima, naturalmente, aparecerá donde r sea máximo. El momento polar de inercia se obtiene de la fórmula de Steiner,
|
[5]
|
En la que:
A = Área de la garganta de cada soldadura.
J0 = Momento polar de inercia de la soldadura alrededor de su propio centro de gravedad O`.
r0 = Distancia dedes O` al centro de gravedad O del grupo.
Usando la misma figura 1.3.9 se puede definir el efecto de flexión dado por la fuerza Fz. En este ejemplo se produce flexión respecto a los ejes x y y que pasan por el centroide O determinados segúnn las relaciones My = Fzxd y Mx = Fzxe. Cuando existe simetría geométrica y simetría respecto a las cargas, estos momentos dan origen al cálculo de esfuerzos:
|
[6]
|
Que corresponde a la ecuación de calculos de esfuerzos por flexión cuando la flexión se produce respecto a ejes principales.

Fig. 1.3.10.- Tablero de puente con directriz en arco.
1.3.3.- Resistencia de las uniones soldadas.
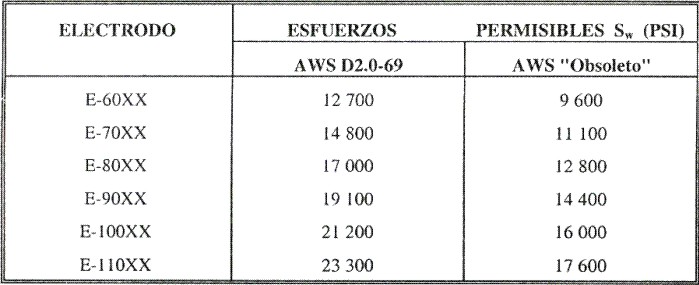
La adaptación de las propiedades de los electrodos a las del metal matriz no es tan importante como la velocidad, la habilidad del operador y el aspecto de la unión completa. Las propiedades de los electrodos varían considerablemente, pero la tabla 1.3.1 relaciona las propiedades mínimas para algunas clases de electrodos.
Tabla 1.3.1.- Propiedades mínimas del metal de soldadura.
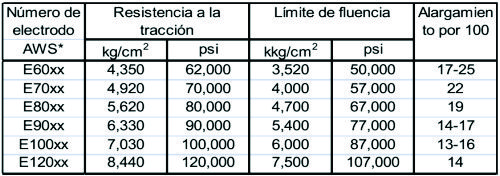
*Sistemas de numeración especificados por la American Welding Society (AWS) para los electrodos. Este sistema emplea un prefijo E delante de un sistema de numeración de cuatro o cinco dígitos, en los que las dos o tres primeras filas designan la resistencia a la tracción aproximada. El último dígito indica ciertas variables en la técnica de la soldadura, como el tipo de corriente. El penúltimo dígito indica la posición de la soldadura como, por ejemplo, plana, vertical o superior.
Es preferible, al proyectar componentes soldados, seleccionar un acero que produzca una rápida y económica soldadura, aunque esto pueda exigir el sacrificio de otras cualidades, tales como su aptitud de mecanización. Bajo condiciones apropiadas, todos los aceros pueden soldarse, pero se obtendrán los mejores resultados si se escogen aceros que tengan unas especificaciones AISI entre C1014 y C1023. Todos estos aceros, cuando están laminados en caliente, tienen una resistencia a la tracción comprendida entre 4.200 y 5.000 k/cm2.
El proyectista podrá escoger coeficientes de seguridad o tensiones de trabajo permisibles con más confianza, si está al tanto de los valores que emplean otros. Una de las mejores especificaciones que se puede empleares la norma para la construcción de edificios del American Institute of Steel Construction (AISC), que se ha revisado recientemente.
Las tensiones permisibles se basan ahora en el límite defluencia en vez de en el límite de rotura, y la norma permite el empleo de una diversidad de aceros estructurales ASTM, con límites de fluencia variables desde 2300 a 3500 kg/cm2. Con tal de que los esfuerzos sean los mismos, la norma permite la misma tensión en el metal de la soldadura y en el metal base. Para estos aceros ASTM Sy =0.5*Sµ. La tabla 1.3.2 relaciona las fórmulas especificadas por la norma para poder calcular estas tensiones permisibles endiversas condiciones de carga. Los coeficientes de seguridad que emplea esta norma se calculan fácilmente. Para tracción n = 1/0.60 = 1.67. Para cizalladura n = 0.577/0.40 = 1.44, si aceptamos la teoría de la energía de distorsión como criterio de fallo.
Tabla 1.3.2.- Tensiones permitidas por la norma AISC para el metal de soldadura.
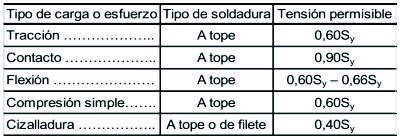
Tanto la norma AISC como la AWS incluyen las tensiones permisibles cuando están presentes cargas de fatiga. El proyectista no tendrá dificultades en emplear estas normas, pero su naturaleza empírica tiende a oscurecer el hecho de que se han obtenido por medio de los mismos conocimientos sobre el fallo por fatiga. Naturalmente, para las estructuras a las que se refieren estas normas, las tensiones reales no pueden exceder a las tensiones permisibles; de otro modo, el proyectista es legalmente responsable. Pero en general, las normas tienden a disimular el margen real de seguridad empleado. Por otra parte, si se emplea el conocimiento total disponible para proyectar, digamos, una máquina, se sabe el margen de seguridad real con cierta precisión y también la dispersión que ha de esperarse. Por tanto, con objeto de recalcar y reforzar las nociones fundamentales, utilizaremos también los métodos en el proyecto de elementos soldados frente a la fatiga.
Los coeficientes de reducción de la resistencia a la fatiga, relacionados en la tabla 1.3.3, fueron propuestos por Jennings y se sugiere su empleo:
Tabla 1.3.3.- Coeficientes de reducción de resistenciaa la fatiga.

1.3.3.1.- Tipología de las uniones soldadas en ángulo.
Uniones soldadas planas: Son aquellas en la que los diferentes cordones están contenidos en el mismo plano o las que permite abatir todas las secciones de garganta sobre un mismo plano.
Uniones soldadas espaciales: Aquellas en la que no es posible abatir sobre un mismo plano todas las secciones de garganta de los distintos cordones que las componen.
Uniones mixtas: Aquellas uniones constituidas por soldaduras de ángulo y soldaduras a tope.
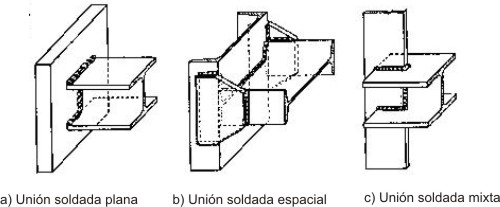
Fig. 1.3.10
1.3.3.2.- Esfuerzos permisibles en uniones soldadas.
1.3.3.2.1.- Se toman igual al metal base en los siguientes casos:.
Para elementos sometidos a esfuerzos de tracción ó compresión paralelo al eje del cordón soldado a tope con penetración completa.
Para elementos sometidos a esfuerzos de tracción, normal al cordón soldado a tope con penetración completa.
Para elementos sometidos a esfuerzos de compresión, normal al cordón soldado a tope con penetración completa ó parcial.
Para elementos sometidos a esfuerzos de corte en la garganta de un cordón soldado a tope con penetración completa ó parcial.
1.3.3.2.2.- De acuerdo a la especificación AWS D2.0-69, se puede tomar:
Para los siguientes casos:
Para elementos sometidos a esfuerzos de corte en la garganta efectiva de un cordón de soldadura de filete paralelo a la dirección de la carga (carga longitudinal).
Para elementos sometidos a esfuerzos de tracción, normal al cordón soldado a tope con penetración parcial.
Para elementos sometidos a esfuerzos de corte en el área efectiva de una soldadura de tapón.
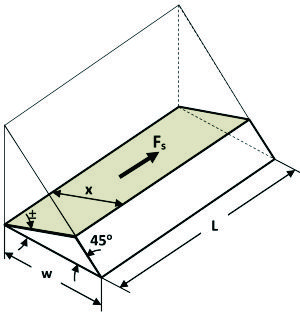
Fig. 1.3.11
Ver: Tabla de recomendación de uso de electrodos.
1.3.3.2.3.- Esfuerzos permisibles en cordones de soldadura de filete, referido a los lados del filete.
En caso de no disponer de soldador calficado preferible sería utilizar:
Para E-60XXX: Ss = 13 600 PSI
Para E-70XXX: Ss = 15 800 PSI
En caso contrario utilizar la siguiente tabla:
Fuente: MSC.Ing. Fortunato Alva Davila - Diseño de Elementos de Máquinas I
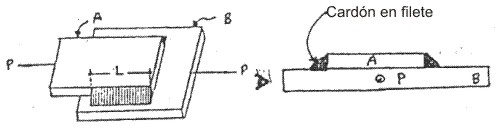
1.3.3.3.- Unión Traslapada o en ángulo.- Llamado también de filete con soldadura de cordón, se presenta en dos formas según la acción de la carga.
1.3.3.3.1.- Unión Traslapada con cargas concéntricas.- Llamados uniones a superposición o superpuestas, se observa que la carga P no actúa en forma colineal en ambas planchas, debido a que una está sobre otra, entonces el llenado de de la soldadura se hará en forma angular:
Fig. 1.3.12
El pequeño par que pueden producir las cargas P al no ser colineales son despreciables si es que la soldadura es uniforme en todo el cordón de llenado.
En estas uniones la falla se produce generalmente en una rectángulo cuyo lado mayor es la longitud del cordón soldada y el lado menor es la altura del triángulo isósceles respecto a la hipotenusa.
Fig. 1.3.13
De donde:
Donde:
L = Lw = longitud efectiva del cordón.
P = carga permisible.
SS = esfuerzo de corte permisible.
Si el cordón está soldado por dos lados de una de las planchas:
Fig. 1.3.14
La carga P está soportado por ambos lados, se duplica el área del rectángulo.
1.3.3.3.2.- Unión traslapada con cargas excéntricas.- Este tipo de uniones son los que traen mayores dificultades para calcular la resistencia de una estructura soldada, se presentan tres casos:
a).- Carga de corte directo. Considerando la carga aplicada actúa en el centro de gravedad y en el plano del cordón de soldadura de filete, la carga de corte por unidad de longitud del cordón será:
Donde:
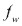
Carga de corte por unidad de longitud.
- P
Carga actuante.
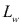
Longitud efectiva del cordón.
b).- Cargas que generan momento flector.- Viendo la figura siguiente, en este caso no se produce tracción como es el caso de los remaches, sino corte, ya que se trata de una masa fundida.
Fig. 1.3.15
Lo cual genera:
i).- Carga de corte directo.- En función de la longitud efectiva:
ii).- Carga de corte secundario debido al momento flector. Cuando el momento flector actúa en el eje “x” y/o “z” que pasa por el centro de gravedad del cordón de soldadura, la carga de corte por unidad de longitud del cordón será:
Donde:
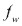
Carga de corte por unidad de longitud.
- M
Momento flector actuante.
- r
Distancia del eje del centro de gravedad al extremo del cordón.
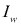
Momento de inercia de línea con respecto a uno de los ejes coordenados.
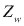
Módulo de línea.
También se puede descomponer la carga secundaria en las direcciones horizontal(x), como vertical(z), haciendo:
c).- Cargas que generan momento torsor.
Fig. 1.3.16
i).- Carga de corte directo.- En función de la longitud efectiva:
ii).- Carga de corte secundario debido al momento torsor: Cuando el momento de torsión actúa en el eje que pasa por el centro de gravedad del cordón de soldadura, la carga de corte por unidad de longitud del cordón será:
Donde:
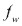
Carga de corte por unidad de longitud.
- T
Momento torsor actuante.
- r
Distancia del eje del centro de gravedad al extremo más alejado del cordón.
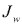
Momento de inercia polar de línea.
1.3.3.3.3.- Carga resultante de corte.
Para el caso de cargas que actúan en planos mutuamente perpendiculares:
1.3.3.3.4.- Tamaño del cordón de soldadura de filete.
1.3.3.3.5.- Cordones de soldadura de filete intermitente.
Se puede hacer uso de cordones intermitente cuando por cálculo, el tamaño del cordón resulta ser pequeño, por debajo del valor mínimo recomendado. Para estos casos, la intermitencia se calcula por la expresión:
La tabla (4) permite seleccionar el paso y la longitud de los codones de soldadura.
1.3.3.3.6.-Recomendaciones generales.
El tamaño mínimo del cordón de soldadura de filete, en lo posible deberá estar sujeto a lo indicado en la tabla (2).
El tamaño máximo de un cordón de soldadura de filete soldado a lo largo de los bordes a unir será:
Para:
Para elementos redondeados el tamaño máximo debe ser la 3/4 de su espesor.
Donde sea posible, el cordón de soldadura de filete debe terminar "doblando una esquina" con una longitud no menor de 2W, en especial, en cordones sometidos a cargas excéntricas.
La longitud efectiva de un cordón de soldadura de filete es la longitud total del cordón de tamaño completo, incluyendo la longitud "doblada en una esquina".
La longitud efectiva mínima de un cordón de soldadura de filete debe ser:
La longitud efectiva de un segmento de cordón de soldadura de filete en cordones intermitentes, deberá ser:
, y no menor de 1 1/2".
El traslape mínimo en cordones de soldadura de filete deberá ser:
y no menor de 1". Siendo t = espesor de la plancha más delgada.
Cuando se requiera tener la resistencia completa por medio de cordones de soldadura de filete a ambos lados con metales bases de espesores diferentes. es necesario que: W = 0.75 t. Siendo t = espesor de la plancha más delgada
Cuando se diseñe un miembro que sirve solamente para dar rigidez y no se pueda evaluar las cargas que actúan sobre él, se puede considerar: W = 0.25 t a W = 0.375 t, para cordones soldados ambos lados. También puede hacer uso de cordones intermitentes de tamaño completo, equivalente al valor recomendado.
Para el caso de vigas fabricadas de ala ancha, se recomienda:
. Siendo, t = espesor del alma.
1.3.3.4.-Cordones de soldadura sometidos a cargas de fatiga.
El cálculo de cordones de soldadura de filete sometido a cargas de corte variable en función al tiempo es similar a otros elementos sujetos a fatiga, y está dado por laexpresión:
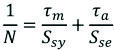
Siendo:
![]()
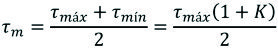
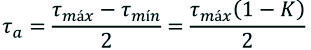
Se obtiene:
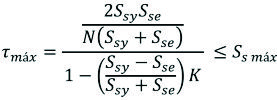
El esfuerzo de corte máximo admisible por fatiga se puede escribir:
![]()
Siendo:
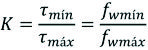
La tabla (5) indica los valores de los esfuerzos admisibles para varias situaciones de cargas.
1.3.3.5.-Tablas.
Ver Tablas (Fuente: Diseño de Elementos de Máquinas del MSc. Ing. Fortunato Alva Davila)