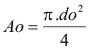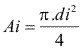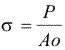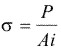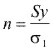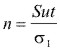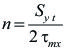2.- MATERIALES DE FABRICACIÓN.
En todo diseño la selección de los materiales es de fundamental importancia, por lo que es necesario tener conocimientos básicos de materiales, metalurgia, tecnologías mecánicas, etc. Es necesario conocer el comportamiento de los diferentes tipos de materiales frente a la acción de agentes externos tales como: esfuerzos, temperatura, oxidación, etc. y también de su correspondiente composición química, estructura interna, etc.
Material, son sustancias homogéneas, de las cuales se construyen los elementos. Los materiales para construir elementos se eligen de acuerdo a sus propiedades.
Materiales en ingeniería y sus propiedades mecánicas. (Recuperado de https://youtu.be/B7qSem5z6mw)
2.1.- Propiedades de los Materiales.

Fig. 2.1
Las propiedades de los materiales que se deben tomar en cuenta, son:
2.1.1.- Sensoriales.- Relacionadas al efecto que producen en nuestros sentidos: textura, olor, forma, brillo, color.
2.2.1.- Termo - Eléctricas.- Relacionadas principalmente a su capacidad de conducir o resistir el calor y/o la electricidad.
2.3.1.- Químicas.- Relacionadas a la resistencia del material a la oxidación, corrosión, etc.
2.2.4.- Mecánicas.- Referidas a la forma en que reaccionan los materiales cuando actúan fuerzas sobre ellos.
Las propiedades mecánicas y tecnológicas son las más importantes y se muestran en la siguientes figuras:
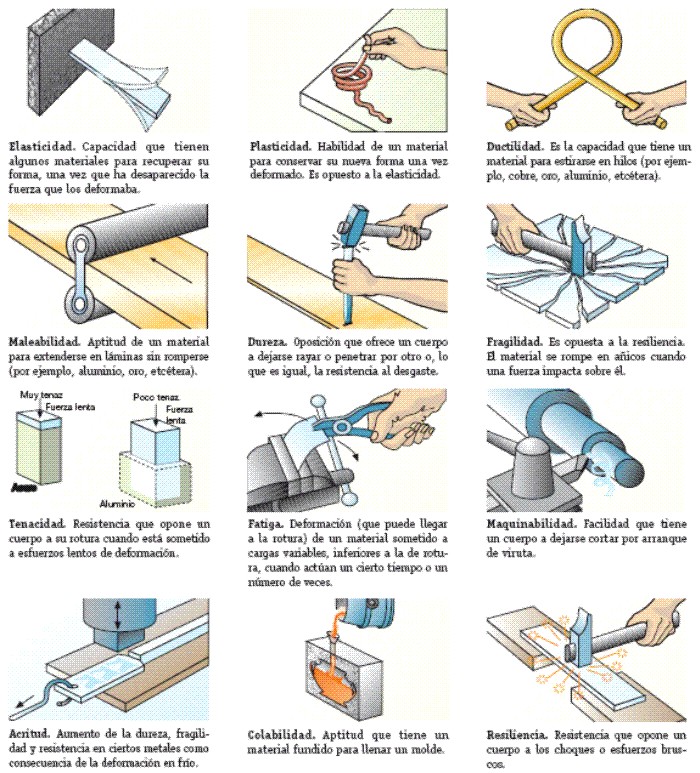
Fig. 2.2
2.2.- Esfuerzos físicos a los que pueden someterse los materiales.- Cuando una fuerza actúa sobre un objeto, tiende a deformarlo. La deformación producida dependerá de la dirección, sentido y punto de aplicación donde esté colocada esa fuerza.
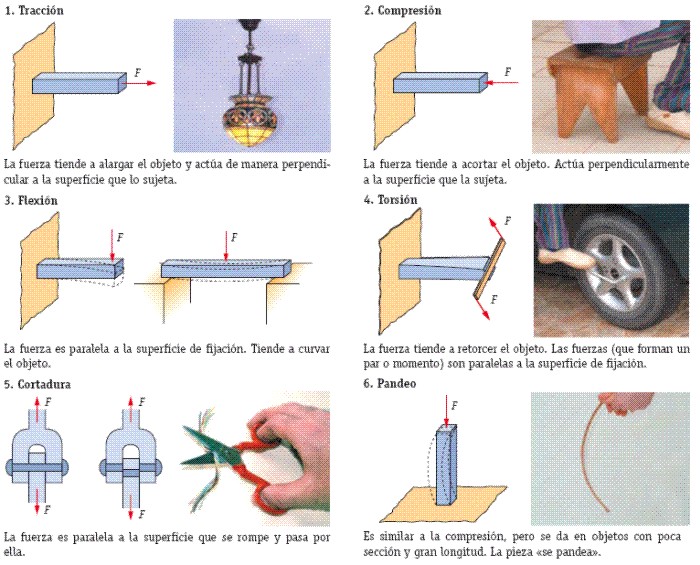
Fig. 2.3
CLASE 1 - DISEÑO DE ELEMENTOS DE MÁQUINAS (Recuperado de https://youtu.be/7BROi5IC1cQ)
CLASE 2- DISEÑO DE ELEMENTOS DE MÁQUINAS (Recuperado de https://youtu.be/TS10wjaahKY)
CLASE 3 ESFUERZO NORMAL DE TENSIÓN Y COMPRESIÓN | DISEÑO DE ELEMENTOS DE MÁQUINAS (Recuperado de https://youtu.be/HBcbNuohAC4)
CLASE 4 ESFUERZO NORMAL debido a LA CARGA AXIAL y ESFUERZO CORTANTE (Recuperado de https://youtu.be/kZbKQFotLf0)
2.3.- Ensayos en Materiales.- Con objeto de averiguar si un material es más adecuado para soportar alguno o varios de los esfuerzos estudiados anteriormente, se le somete a una serie de pruebas en las que se determina cada una de las propiedades mecánicas, así como la resistencia a un determinado esfuerzo.
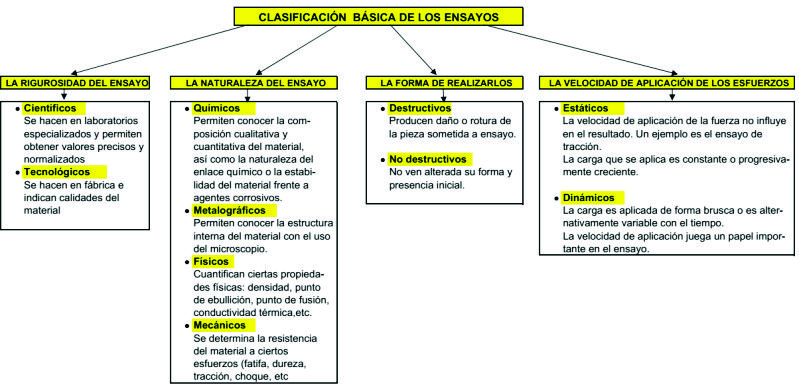
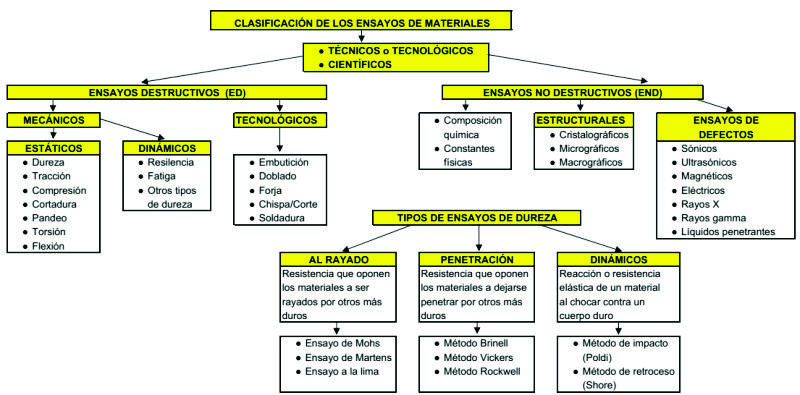
Fig. 2.4
Algunos de los muchos ensayos empleados se muestran a continuación:
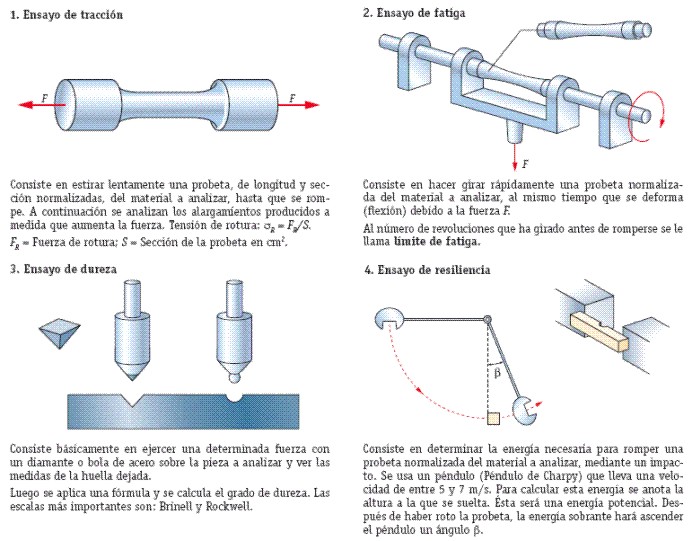
Fig. 2.5
2.3.1.- Ensayo de tracción
Ensayo de tracción - UPV (Recuperado de https://youtu.be/-5CStao_C2U)>
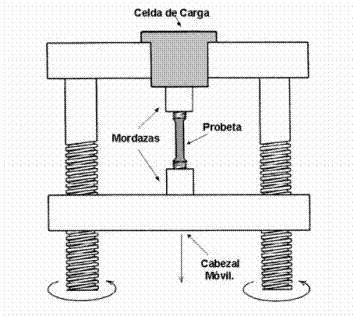
Es una de las más comunes de los ensayos para conocer las cargas que pueden soportar los materiales, se efectúan ensayos para medir su comportamiento en distintas situaciones. El ensayo destructivo más importante es el ensayo de tracción, en el que se coloca una probeta en una máquina de ensayo provista de dos mordazas, una fija y otra móvil. Se procede a medir la carga mientras se aplica el desplazamiento de la mordaza móvil. Un esquema de la máquina de ensayo de tracción se muestra en la Figura 2.4
Fig. 2.4. Máquina de ensayo de tracción |
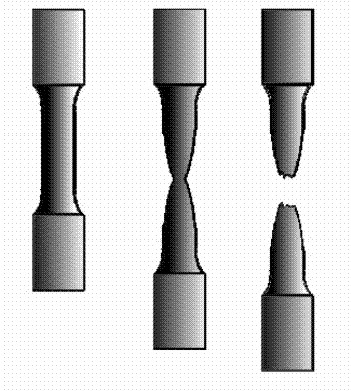
Fig. 2.5. Probeta antes y después del ensayo |
La máquina de ensayo impone la deformación desplazando el cabezal móvil a una velocidad elegible. La celda de carga conectada a la mordaza fija entrega una señal que representa la carga aplicada, las máquinas poseen un dibujante mecánico que grafica en un eje el desplazamiento y en el otro eje la carga leída.
La figura 2.5, muestra la forma de la probeta al inicio, al momento de llegar a la carga máxima y luego de la rotura.
La Figura 2.6 muestra el diagrama típico (esfuerzo-deformación) obtenido en una máquina de ensayo de tracción para un acero.
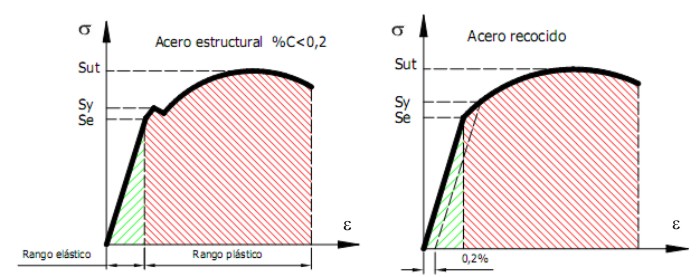
Fig.2.6. Diagrama Esfuerzo-Deformación en aceros dúctiles al carbono.
La gráfica inicialmente está definida por una línea recta (zona elástica), en donde la probeta se comporta literalmente como un resorte, es decir, la probeta se deforma de manera uniforme ante la carga aplicada y si esta se suprime, la probeta regresa a su longitud inicial. La zona elástica inicia en el origen y termina en el punto p (punto de proporcionalidad), hasta el cual se cumple la ley de Hooke:
![]()
Donde:
![]() : Esfuerzo normal
: Esfuerzo normal
E: Módulo de elasticidad
![]() : Deformación
: Deformación
Después de alcanzar el punto p, existe una pequeña zona, todavía elástica, que se desvía ligeramente de la línea de proporcionalidad hasta alcanzar el punto E (punto de elasticidad), en la cual ya no se cumple la ley de Hooke. A partir de la zona elástica, el material comienza a deformarse de forma permanente, es decir, si se suprime la carga, la probeta no retorna a su tamaño original. Por definición se ha alcanzado la zona plástica del ensayo de tracción. Casi al inicio de la zona elástica, existe un punto, en el cual el material comienza a deformarse de forma considerable sin el aumento correspondiente de carga, denominado punto de cedencia o fluencia (yield point). La resistencia en ese punto se designa como Sy, resistencia a la fluencia.
Luego de la fluencia, la gráfica continúa con un ascenso lento en el esfuerzo, pero significativo en la deformación, hasta llegar a un punto máximo, denominado esfuerzo máximo , ó, de forma más común, esfuerzo último a la tensión, designado como Sut. La probeta se alarga en forma permanente hasta la rotura.
El área bajo la curva Esfuerzo-Deformación (![]() vs
vs ![]() ) representa la energía disipada durante el ensayo, es decir la cantidad de energía que la probeta alcanzó a resistir. A mayor energía, el material es más tenaz.
) representa la energía disipada durante el ensayo, es decir la cantidad de energía que la probeta alcanzó a resistir. A mayor energía, el material es más tenaz.
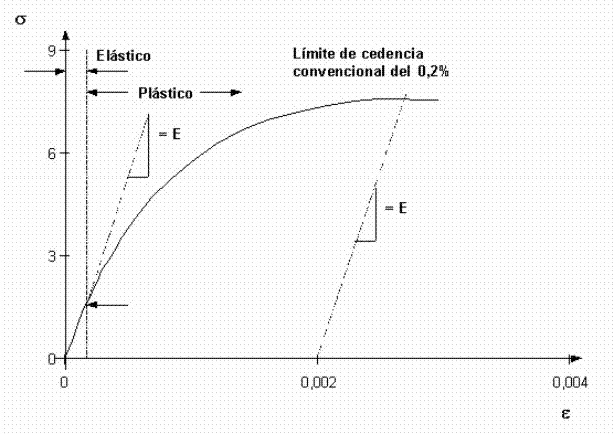
Fig. 2.7.- Método de corrimiento Off.Set para calcular límite de fluencia.
Finalmente, si la curva (![]() vs
vs ![]() ) del material no presenta claramente dónde termina la zona elástica y comienza la zona plástica, se define como punto de fluencia al esfuerzo correspondiente a una deformación permanente del 0,2%. La figura 2.7, ilustra lo anterior, mostrando el método de corrimiento Off-Set, para hallar de forma gráfica el límite de fluencia para una deformación permanente de 0,2%.
) del material no presenta claramente dónde termina la zona elástica y comienza la zona plástica, se define como punto de fluencia al esfuerzo correspondiente a una deformación permanente del 0,2%. La figura 2.7, ilustra lo anterior, mostrando el método de corrimiento Off-Set, para hallar de forma gráfica el límite de fluencia para una deformación permanente de 0,2%.
Para obtener un diagrama esfuerzo-deformación, como el mostrado en la figura 5, se requiere aplicar una serie de ecuaciones en las cuales intervienen los datos tomados en laboratorio, los cuales se ordenan como en la tabla 2.1. Estas ecuaciones se presentan a continuación, especificando su aplicación en cada columna de la tabla.
Tabla 2.1. Parámetros Requeridos para Elaborar el diagrama esfuerzo-deformación
| Datos de Laboratorio | Columna |
| Pi = carga aplicada a la probeta (variable durante el ensayo) | 1 |
| lo = longitud calibrada original | 2 |
| li = longitud calibrada bajo carga (varía por efecto del ensayo) | 2 |
| do = diámetro calibrado original | 3 |
| di = diámetro bajo carga Pi (varía por efecto del ensayo) | 3 |
| Cálculos | |
| Ao = área transversal original | 4 |
| Ai = área transversal bajo la carga Pi | 4 |
| 5 | |
| 7 | |
| 6 | |
| 6 | |
| 8 | |
| 8 | |
|
|
|
|
Ingeniería:
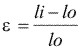 (Hasta segunda variación del área), luego:
(Hasta segunda variación del área), luego: 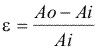
Verdaderos:
 (Hasta segunda variación del área), luego:
(Hasta segunda variación del área), luego: 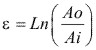
Tabla 2.2

2.3.2.- Ensayo de Flexión (Ver video)
Ensayo de Flexión (Recuperado de https://youtu.be/rjQuM7Nu1tI)>
2.3.3.- Ensayo de Torsión (Ver video)
Ensayo de Torsión (Recuperado de https://youtu.be/MKFi6GAaMo0)>
2.3.4.- Ensayo de Fatiga (Ver video)
ENSAYO DE FATIGA (Recuperado de https://youtu.be/debxQ8a4kTc)>
2.3.5.- Ensayo de dureza
ENSAYOS de DUREZA - Rockwell, Brinell, Vickers y Knoop (Recuperado de https://youtu.be/mQZqq1Ql2ts)>
Los métodos más usados para determinar la dureza son el Brinell y Rockwell aunque los métodos de Vickers y de microdureza Knoop también tienen aceptación. Existe además el método del escleroscopio Shore. Todos estos método, con exepción de el escleroscopio, consisten en presionar con una pieza bastante dura, durante un tiempo determinado, sobre la superficie del material que se ensaya. Finalmente se aplica una fórmula en función de la carga y la indentación para hallar el valor de la dureza. La importancia de la dureza Brinell es su relación directa con la resistencia última a la tensión, en kpsi, de los aceros (HB = 2.Sut).
Brinell: 10 segundos una bola de acero de d = 10 mm.
|
Carga P = 3000 Kgf Carga P = 500 Kgf |
acero metales blandos |
Rockwell: Utiliza una esfera de acero de diferentes diámetros y un cono de diamante. Cada uno de ellos con diferentes cargas.
El escreroscopio Shore consiste en dejar caer un martillo sobre el material ensayado, y en función de la altura que alcance éste, después del rebote, se obtiene el valor de la dureza con el apoyo de una tabla.
2.4.- Clase de Materiales
2.4.1.- De origen vegetal o animal.
Entre los más usados en maquinaria agrícola tenemos:
a).- Madera.- Se caracteriza por ser de resistencia estructural media, bajo costo y fácil procesamiento para construir mecanismos o máquinas. La madera es un compuesto de fibras largas de celulosa sujetas en una matriz resinosa de lignina, y por ello tiene alta flexibilidad.
b).- Cuero.- Proviene de los animales. Antes de ser empleado se le somete a un proceso de curtido para asegurar su resistencia al intemperismo.
c).- Goma natural.- Proviene del árbol del caucho. Adicionándole azufre se transforma en caucho blando (adición de 2-20% de azufre) o caucho duro (adición de 30-50% de S).

Figura 2.8. Madera y goma natural empleadas en la construcción de maquinaria.
2.4.2.- Metálicos Ferrosos.
|
¿Qué es un metal? Se denomina metal a los elementos químicos caracterizados por ser buenos conductores del calor y la electricidad. Poseen alta densidad y son sólidos en temperaturas normales (excepto el mercurio); sus sales forman iones electropositivos (cationes) en disolución. Metales Ferrosos Los Metales Ferrosos son aquellos que, su principal componente es el HIERRO y, sus principales características son su gran resistencia a la tensión y dureza. A pesar de todos los inconvenientes que presentan estos materiales (hierro, acero y fundiciones) por ser muy pesados, oxidarse con facilidad y ser difíciles de trabaja, entre otros, son uno de los más usados en la actualidad. |
MATERIALES FERROSOS (Recuperado de: https://youtu.be/VG7x3sIy6OI) |
Los metales ferrosos son los:
- Acero
- El hierro
- Las fundiciones
Tipos de metales ferrosos:
Hierros: son productos ferrosos cuyo porcentaje de carbono está comprendido entre el 0.01 - 0.03 %. Son muy blandos y difíciles de obtener.
Aceros: son aleaciones de hierro y carbono (porcentaje de carbono: 0.03 - 1.76 %).
Fundiciones: son aleaciones de hierro y carbono (porcentaje de carbono: 1.76 - 6.67 %).
Grafitos: son aleaciones que se obtienen cuando el porcentaje de carbono es superior al 6.67 %.
a).- Hierro.- El hierro es un metal de transición con características muy particulares, es uno de los elementos más abundantes en la corteza terrestre y más aún en el núcleo de la Tierra. Al ser tan abundante, dúctil y resistente, se usa en diversas actividades humanas.
El hierro por si solo no tiene demasiados usos, pero es muy importante ya que al alearse con cualquier metal o no metal adquiere diversas propiedades para determinados usos.
Ver videos sobre metales:
b).- Acero.- Se caracteriza por su alta resistencia estructural.
Webinar: Introducción a los Aceros al Carbono (Recuperado de https://youtu.be/I6ogNLeMvj8)
Existen diversas aleaciones de acero que le dan características especiales por ejemplo con manganeso tiene alta resistencia al choque, con níquel tenacidad, con cromo es duro e inoxidable.
Aceros Aleados:
Cromo: Origina formación carburos cromo y refina estructura de grano. Aumenta tenacidad y dureza.
Níquel: Produce mejor núcleo. Mejora Sy y Sut sin reducir ductilidad.
Manganeso: Disuelve ferrita y forma carburo cromo.
Cromo: Origina formación carburos cromo y refina estructura de grano. Aumenta tenacidad y dureza.
Silicio: Desoxidante. Material frágil y estabiliza carburos.
Molibdeno: Se usa con otros elementos de aleación. forma carburos y disuelve la ferrita. alta tenacidad.
Vanadio: forma carburos y tamaño fino de granos. Acero para herramientas.
Tungsteno: produce estructura fina y densa. Aumenta tenacidad y dureza conservándola aun al rojo vivo.
Para designar los distintos tipos de acero, la AISI/SAE (American Iron and Steel Institute/ Society of Automotive Engineers) utiliza un sistema de 4 dígitos, donde los dos primeros dígitos indican los elementos de aleación principales y los dos últimos indican la cantidad de carbono presente, expresada en centésimas de porcentaje. Ver Cuadro 02
Tabla 2.3. DESIGNACIONES AISI/SAE DE ALEACIONES DE ACERO
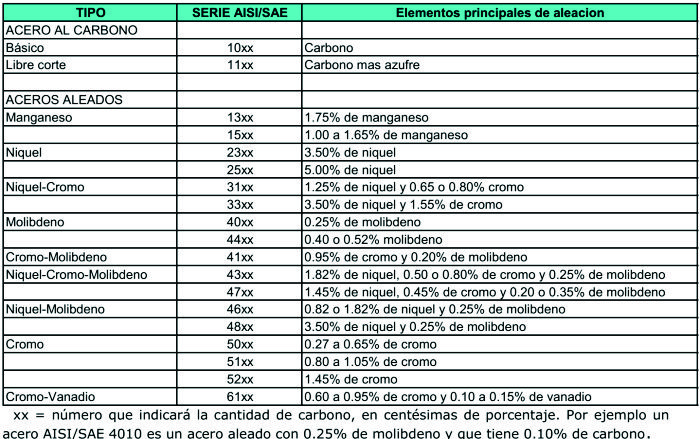
Otra entidad que emite estándares para el acero es la American Society for Testing of Materials (ASTM).
2.4.3.- Metálicos No Ferrosos.- Comprende todos los metales a excepción del hierro.
- Su utilización no es tan masivas como los productos férreos (hierro, acero y fundición) pero tienen una una gran importancia en la fabricación de gran cantidad de productos, por propiedades como, en ocasiones:
- El bajo peso específico.
- La resistencia a la oxidación condiciones ambientales normales.
- La fácil manipulación y mecanizado.
- Las aleaciones de productos no ferrosos tienen gran cantidad de aplicaciones:
- Monedas (fabricadas con aleaciones de cobre, níquel y aluminio).
- Filamentos de bombillas (de wolframio).
- Material de soldadura de componentes electrónicos (estaño-plomo).
- Recubrimientos (cromo, níquel, zinc).
- Etc.
- En general, los metales no ferrosos son blandos y tienen poca resistencia mecánica. Para mejorar sus propiedades se alean con otros metales.
Atendiendo a su densidad, se pueden clasificar en:
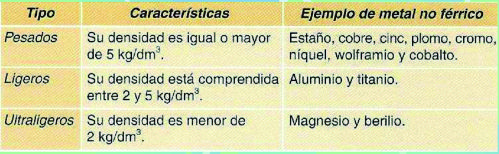
Los metales no ferrosos, ordenados de mayor a menor utilización, son:
- Cobre(y sus aleaciones).
- Aluminio.
- Estaño, plomo.
- Zinc.
- Níquel.
- Cromo.
- Titanio.
- Magnesio.
Metales no ferrosos 1 (Recuperado de: https://youtu.be/06V7wGqwFHI)
Metales no ferrosos 2 (Recuperado de: https://youtu.be/ha1S_CPddYQ)
a).- Cobre.- Tiene alta conductividad térmica y eléctrica y no es magnético. Su aleación con Zinc produce el latón, y con estaño produce el bronce.
b).- Zinc.- Tiene resistencia a la corrosión. Es tóxico para humanos. Se utiliza para galvanizar metales (resistencia al oxidamiento).
c).- Estaño.- Tiene resistencia a la corrosión.
d).- Plomo.- Resistente a la corrosión por acción de los ácidos, es tóxico.
e).- Aluminio.- Tiene buena conductividad térmica y eléctrica (aunque menor a la del cobre). Aleado con silicio y magnesio se usa en culatas y pistones de motores. Es el metal no ferroso de mas amplio uso.
f).- Sinterizados.- Cuando los materiales no se pueden unir por fundición, se usa el sinterizado.
Materiales sinterizados (Recuperado de: https://youtu.be/i-S8E7AkBi8)
2.4.4.- Materiales Sintéticos.
Materiales Sintéticos (Recuperado de https://youtu.be/MmR2xG9utWU).
Actualmente, el uso de materiales no metálicos en la construcción de maquinaria se incrementa rápidamente. Hay 3 categorías de materiales sintéticos de interés:
a).- Polimeros (plasticos).- Se fabrican a partir del petróleo o el carbón. Se caracterizan por tener peso reducido, resistencia mecánica baja, alta resistencia a la corrosión, alta resistencia dieléctrica, facilidad de manufactura y un costo bajo.
Termoplastes.- Material flexible y moldeable por calentamiento por ejemplo polivinilo de cloruro (PVC), polietileno, polystirol, poliamidas, vidrio acrílico.
Elastómeros.- Material elástico que se deja vulcanizar por ejemplo el caucho sintético utilizado en neumáticos.
Duroplaste.- Material que se puede endurecer por calentamiento. Una vez formados, no pueden ser recalentados para moldearlos con otra forma. por ejemplo melamina.

Figura 2.9. Bandeja para plantines (termoplaste), llantas (elastómeros), casco (duroplaste).
b).- Ceramicos.- Los materiales cerámicos de ingeniería suelen ser compuestos de elementos metálicos y no metálicos. Pueden ser únicamente un óxido de un metal, mezclas de óxidos metálicos, carburos, boruros, nitruros y otros elementos como el Al2O3, el MgO, el SiC y el Si3N4. Tienen una resistencia a la compresión bastante alta, elevada resistencia al desgaste por abrasión, durabilidad química y resistencia a altas temperaturas.
Materiales Cerámicos (Ingeniería de Materiales) (Recuperado de https://youtu.be/BPntqAvfUxc)
Son demasiado duros para maquinar mediante técnicas convencionales, y por lo general son formados por compactación de polvos y después quemados o sinterizados para formar enlaces entre partículas, lo que incrementa su resistencia. A menudo se utilizan compuestos cerámicos rociados por plasma como recubrimiento duro sobre sustratos metálicos, a fin de obtener superficies resistentes al desgaste y la abrasión.
Se les utiliza en diversos elementos como: rotores de turbocargadores, armaduras ligeras, válvulas de los caños de agua, herramientas cortantes, cojinetes de bolas, elementos refractarios y elementos sometidos a desgaste como pistones, cilindros, rejas, discos, etc.

Figura 2.10. Diversos elementos construidos con material cerámico.
c).- Compuestos.- Suelen ser una combinación de un material resistente y fibroso (como el vidrio, el grafito o las fibras de boro) cementado en una matriz de resina, como un epoxi o un poliéster. Pueden tener cualquier combinación de propiedades que se desee.Los materiales compuestos tienen uso en aplicaciones d alto esfuerzo dadas sus elevadas razones resistencia/peso.
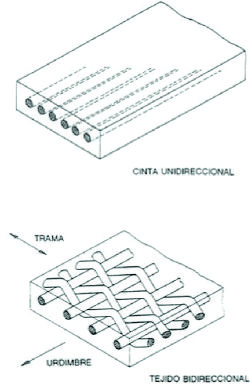
Figura 2.11. Estructura de un material compuesto.

Figura 2.12. Espaciador construido del material compuesto MEGALIFEXT, resiste esfuerzos hasta de 140 N/mm2.
d).- Materiales Inteligentes.- Son materiales que responden a cambios en: temperatura, humedad, pH, campos magnéticos o eléctricos.
¿Qué son los materiales inteligentes del futuro? (Recuperado de https://youtu.be/34wHqgiXzq4)
Al momento los materiales inteligentes de mayor desarrollo son:
Materiales piezoeléctricos.- Se caracterizan por un cambio de forma rápido y lineal en respuesta a un campo eléctrico. Se usan para trabajar con sonido, como en los pequeños auriculares de teléfonos celulares.
Materiales electroestrictivos y magnetoestrictivos.- Materiales que cambian en tamaño en respuesta a un campo eléctrico o magnético, y que producen un voltaje cuando se estiran.
Materiales reológicos.- Cambian su forma instantáneamente cuando se les aplica una carga eléctrica o magnética.
Materiales Termo Responsivos o Aleaciones con Memoria de Forma.- Son materiales que reaccionan a cambios en temperatura. Por ejemplo un pedazo recto del alambre SMA, llamado Nitinol (aleación de niquel y titanio), puede ser doblado a cualquier forma. Si lo calentamos a 90 oC, el alambre vuelve a su forma recta original.
Materiales Sensitivos al pH.- Cambian su color según el pH.
Materiales Electro-Crómicos.- Cambian sus propiedades ópticas cuando se les aplica un voltaje.
Fullerenes.- Moléculas esféricas encapsuladas con átomos de carbono en las esquinas de estructuras poliédricas consistentes de pentágonos y hexágonos.
Gels Inteligentes.- Gels que se encogen o hinchan por un factor hasta de 1 000, y que pueden ser programados para absorber o liberar fluidos en respuesta a un estimulo físico o químico.

Figura 2.13. Alambre Nitinol con memoria de forma.
Los Sistemas de Materiales Inteligentes, son sistemas estructurales hechos por el hombre inspirándose en modelos de la naturaleza.
Los sistemas naturales tienen muchas cualidades: precisión, eficacia, funcionalidad, durabilidad y adaptabilidad; las que son emuladas por los sistemas de materiales inteligentes. Para lograrlo se utilizan 03 herramientas básicas:
Sensores.- Aálogos al sistema nervioso del hombre, sirven para registrar información interna y externa de importancia.
Actuadores (motores).- Hacen un trabajo similar al de los músculos.
Centros de control computarizados.- Actúan como el cerebro del sistema, tomando decisiones en base de la información que reciben de los sensores, y emitiendo ordenes a los actuadores.

Figura 2.14. Sistema de control inteligente, que mantiene la posición de las boquillas de una asperjadora, a una altura constante sobre las plantas.
2.5.- Tratamiento Térmicos del Acero
Tratamiento térmico del acero. templado, revenido, recocido y normalizado (Recuperado de https://youtu.be/aJKfyJCRQSM)
Tratamientos térmicos del acero: recocido, normalizado, temple y revenido (Recuperado de https://youtu.be/lABq26BapwA)
El tratamiento térmico se refiere a acciones con las que se interrumpe o varía el proceso de transformación descrito por el diagrama de equilibrio. Otras operaciones químicas se agrupan algunas veces bajo el nombre de tratamiento térmico. Las operaciones comunes de tratamiento son: recocido, templado, revenido y templado superficial.
2.5.1.- Recocido: Cuando un material se somete a trabajo en frío o en caliente, se inducen esfuerzos remanentes o residuales y, además, el material generalmente adquiere una gran dureza debida a estas operaciones de labrado. Tales acciones cambian la estructura del material, de modo que ya no queda representada por el diagrama de equilibrio. El recocido es una operación de calentamiento que permite que se transforme el material de acuerdo con el diagrama de equilibrio. El material por recocer se calienta a una temperatura que está aproximadamente a 55ºC sobre la temperatura crítica. Se mantiene esta temperatura por un tiempo suficiente para que el carbono se disuelva y difunda a través del material. El objeto tratado se deja enfriar luego lentamente, por lo general en el mismo horno en el que fue tratado. Si la transformación es completa, se dice entonces que se tiene un recocido total. El recocido se emplea para suavizar un material y hacerlo más dúctil, para eliminar esfuerzos remanente y para refinar la estructura del grano.
2.5.2.- Normalizado: Las piezas que han de normalizarse pueden ser calentadas a una temperatura un poco más alta que la del recocido total. Esto produce una estructura granular más gruesa, que es más fácilmente maquinada si el material es un acero de bajo carbono. En el proceso de normalizado la pieza se enfría en aire tranquilo a la temperatura del ambiente. Puesto que este enfriamiento es más rápido que el lento que se usa en el recocido total, se dispone de menos tiempo para el equilibrio y el material queda más duro que el acero totalmente recocido. El normalizado se utiliza con frecuencia como la operación de tratamiento final de un acero. El enfriamiento de aire tranquilo equivale a un templado (endurecimiento) lento.
2.5.3.- Templado: El acero eutectoide que se recuece totalmente consiste por completo en perlita, que se obtiene a partir de la austenita en condiciones de equilibrio. Un acero hipoeutectoide totalmente recocido consistirá en perlita más ferrita, en tanto que un acero hipereutectoide en la condición de recocido total consistiría en perlita más cementita. La dureza del acero con un determinado contenido de carbono depende de la estructura que reemplaza a la perlita cuando no se realiza el recocido total.
La ausencia de tal recocido indica una intensidad más rápida de enfriamiento. La rapidez de enfriamiento es el factor que determina la dureza. Una rapidez de enfriamiento controlada en un material caldeado constituye el proceso que recibe el nombre de templado. Un temple (endurecimiento) ligero se obtiene por enfriamiento en aire quieto que, como ya se ha visto, es el que se obtiene en el proceso de normalizado. Las dos sustancias más utilizadas para templar son el agua y el aceite. El templado en aceite es un proceso muy lento, pero evita las grietas de temple que se originan por la expansión rápida del objeto que se trata. El templado en agua se emplea en aceros al carbono y para aceros de baja aleación y de mediano carbono.
La eficacia del endurecimiento depende del hecho de que cuando la austenita se enfría no se transforma instantáneamente e perlita, sino que se requiere tiempo para iniciar y completar el proceso. Puesto que la transformación cesa aproximadamente a 425 ºC, esto puede ser evitado enfriando de manera rápida el material a una temperatura menor. Cuando el material es enfriado rápidamente hasta 200 ºC o menos, la austenita se transforma en una estructura llamada martensita. Esta es una solución sólida sobresaturada de carbono en ferrita, y es la clase de acero más dura y resistente.
Si el acero es enfriado en forma rápida hasta una temperatura entre 200 ºC y 425 ºC, y se mantiene ahí por un tiempo suficientemente largo, la austenita se transforma en un material que por lo general se llama bainita. Esta es una estructura intermedia entre la perlita y la martensita. Aunque hay varias estructuras que pueden identificarse entre las temperaturas dadas, dependiendo de la temperatura que se use, se conocen colectivamente como vainita. Mediante la elección de esta temperatura de transformación se puede obtener casi cualquier variedad de estructura. Tales variantes van desde la perlita gruesa hasta la martensita fina.
2.5.4.- Revenido: Cuando una probeta de acero ha sido endurecida totalmente resulta ser dura y frágil en extremos y con esfuerzos remanentes altos. El acero queda inestable y tiende a contraerse al envejecer. Esta tendencia aumenta cuando la probeta se somete a cargas aplicadas exteriormente debido a que los esfuerzos resultantes contribuyen aun más a la inestabilidad. Dichos procesos internos pueden ser eliminados por un proceso de calentamiento ligero llamado de alivio de esfuerzos, o por una combinación de alivio de esfuerzo y suavizado que se denomina revenido. Después de que la probeta ha sido endurecida totalmente por el templado desde arriba de la temperatura crítica, se recalienta a una temperatura inferior a la crítica durante cierto tiempo y luego se deja enfriar a aire tranquilo. La temperatura a la cual se le recalienta depende de la composición y del grado de dureza o de tenacidad que se deseen. Esta operación de recalentamiento libera el carbono retenido en la martensita, formando cristales de carburo. La estructura obtenida recibe el nombre de martensita revenida.
2.5.5.- Templado Superficial:
El objeto de esta acción de endurecimiento es producir una corteza (o superficie exterior) dura en una probeta o una pieza de acero de bajo carbono, reteniendo al mismo tiempo la ductilidad y la tenacidad en el núcleo. Esto se logra aumentando el contenido de carbono en la superficie, es decir, carburizándola. Pueden utilizarse carburizantes o gaseosos. El proceso consiste en introducir la pieza por carburizar en el seno de un material carburizante durante un tiempo a temperatura establecida, dependiente del espesor de la corteza dura que se desee y de la composición de la pieza. Esta última puede ser luego templada directamente desde la temperatura de carburizado, y revenida, o bien en algunos casos debe ser sometida a un tratamiento térmico doble a fin de asegurar que el núcleo y la corteza estén en las condiciones apropiadas. Algunos de los procesos más útiles de templado superficial son los que se denominan carburizados en paquetes o en gas, nitrurizado, cianurizado, endurecimiento por inducción y endurecimiento a la flama.
2.6.- Sistemas de designación númerica del acero
Existen dos formas de identificar los aceros: la primera es a través de su composición química, por ejemplo utilizando la norma SAE - AISI y ASTM:
Clasificación de aceros (Recuperado de https://youtu.be/77xcdGYE58o)
Tipos de Acero ASTM y UNE EN (Recuperado de https://youtu.be/Chxvxdq9Wkw)
Ejemplos
Tabla 2.4.
|
La Tabla 2.5 relaciona la nomenclatura AISI-SAE con los valores de resistencia, ductilidad y dureza, conceptos que se explicarán más adelante. Sirve para relacionar la composición química y las propiedades mecánicas de los aceros. En las Tablas 2.6 y 27 se entrega información detallada de la composición química de diversas aleaciones listadas en base su número AISI-SAE.
|
Tabla 2.5.- Propiedades Mecánicas. Barras de acero en caliente.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Composición química de los principales aceros al carbono.
Tabla 2.6 : Designación AISI con cuatro componentes
Tabla 2.7 : Designación AISI con ocho componentes
La segunda forma de designar los aceros es a través de su resistencia mecánica en tracción, es el caso de los aceros:
Tabla 2.8
| A37-24ES | A: Acero |
| A44-28ES | ES: Estructural soldable |
| A63-42ES | H: Para hormigón |
La primera cifra indica la resistencia a la tracción en kg/mm2, la segunda cifra indica la resistencia a la fluencia en kg/mm2.
En la siguiente tabla se entregan los valores de resistencia y ductilidad de los aceros para uso estructural y de barras para hormigón armado.
Tabla 2.9
| Grados del Acero |
Resistencia a la tracción Rm |
Límite de fluencia Re |
Alargamiento en 50 mm |
||
| Kgf/mm2 | Mpa | Kgf/mm2 | Mpa | % | |
| A37-24ES | 37 | 363 | 24 | 235 | 22 |
| A42-27ES | 42 | 412 | 27 | 265 | 20 |
| A52-34ES | 52 | 510 | 34 | 324 | 18 |
| A44-28H | 44,9 | 440 | 28,6 | 280 | 16 |
| A63-42H | 64,2 | 630 | 42,8 | 420 | (*) |
(*): (700/Rm) - K >= 8, K es un coeficiente que depende del diámetro nominal de la barra (e) y cuyo valor se indica a continuación.
Tabla 2.10
| e (mm) | : | 8 | 10 | 12 | 16 | 18 | 20 | 22 | 25 | 28 | 32 | 36 |
| K | : | 2 | 1 | 0 | 0 | 0 | 0,5 | 1 | 2 | 3 | 4 | 5 |
Fuente: Norma chilena NCh 203 of. 77
Para poder reconocer un acero al momento de adquirirlo, se utiliza una clave de colores que se pinta en la sección de las barras, se entrega a continuación los códigos de color para los aceros distribuídos por la empresa SABIMET.
Para aluminio, se usa la letra A como prefijo: El primer número después del literal indica el procesamiento. el segundo número indica el grupo de aleación. el tercer número indica el límite de impurezas y los dos últimos señalan tipos de aleaciones especiales.
Tabla 2.11
A0 aleación fundida |
A9 aleación forjada |
Aluminio con pureza 99% |
AX1XXX |
Aleaciones con Cobre |
AX2XXX |
Aleaciones con Manganeso |
AX3XXX |
Aleaciones con Silicio |
AX4XXX |
Aleaciones con Magnesio |
AX5XXX |
Aleaciones con Magnesio y Silicio |
AX6XXX |
Aleaciones con Zinc |
AX7XXX |
Para el bronce y el magnesio se tiene una designación similar al de los metales señalados anteriormente.
2.7.- Tensiones, Deformaciones, Relación Tensiones-Deformaciones.
2.7.1.- Esfuerzos (El alumno ya tiene pleno conocimiento, por que el curso de resistencia de materiales es pre requisito del presente curso).
Figura 2.15.- Animación de las fuerzas y momentos actuantes en los cortes respectivos.
2.7.2.- Fatiga
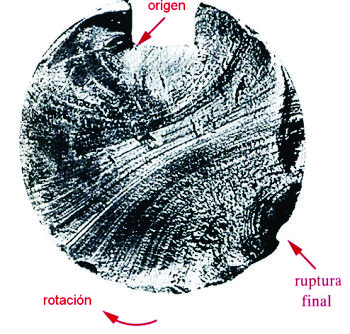
Figura N0 2.16_A Eje rotatorio que presentó falla por fatiga, con inicio de grieta en chavetero del eje
Cada vez son más las partes de piezas que deben ser diseñadas usando el criterio de fatiga. Los esfuerzos variables están casi siempre presente en las máquinas. Ya en el año 1852 el ingeniero alemán Wholer afirmaba: El hierro y el acero pueden romperse bajo un esfuerzo inferior, no sólo al esfuerzo de ruptura estático, sino también inferior al límite elástico, siempre que el esfuerzo se repita un número suficiente de veces. El fenómeno de ruptura bajo cargas variables se denomina Falla por Fatiga.
Las teorías de fatiga clásicas aparecen en toda literatura asociada al diseño de elementos de máquinas. Ocuparemos las pricipales teorías pero debemos contar con material adicional como son las tablas de coeficientes de concentración de esfuerzos. Los principales casos que se usan en la práctica se muestran en la figura 2.15.
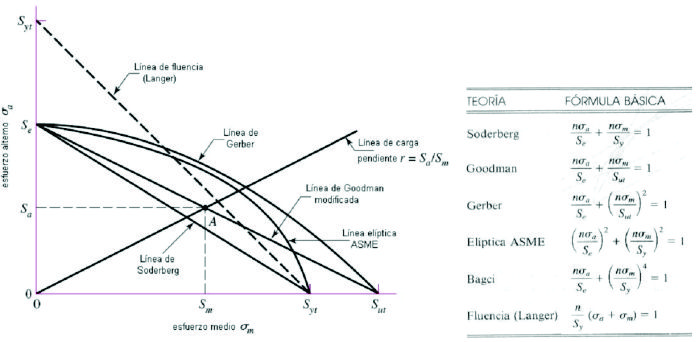
Figura N0 2.16 Criterios de diseño clásicos
Se acepta comúnmente que la falla por fatiga comienza con la formación de una pequeña grieta o fractura que se inicia en un punto (foco), donde existe un alto valor del esfuerzo (concentrador de esfuerzos). Una vez iniciada la fractura, ésta se propaga hasta que la sección resistente de la pieza disminuye a tal grado, que acontece la ruptura.
La superficie de la pieza fracturada por fatiga, normalmente presenta una forma característica, con dos zonas claramente definidas: una zona lisa que corresponde a la zona de propagación de la fisura y una zona granulada que corresponde a la fractura final.
La figura 2.16 corresponde a típicos esfuerzos variables que se asemejan a cargas reales en los elementos.
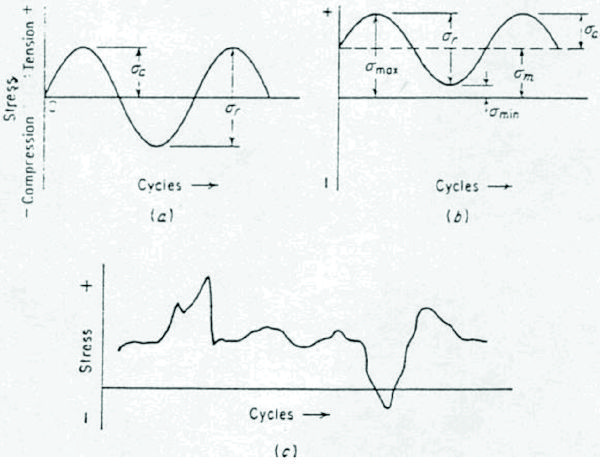
Figura N0 2.17 Modelos de cargas variables
2.7.2.1.- Parámetros que infuyen en la ruptura a la fatiga.
a).- Forma en que se aplican los esfuerzos:
Frecuencia: En general se observa poca variación del límite de resistencia a la fatiga con la variación de la frecuencia de la carga.(2 %)
Forma de aplicación de los esfuerzos: Se ha comprobado que la historia de la carga de la pieza tiene gran importancia en la falla por fatiga.
Tensiones internas o residuales: La distribución de esfuerzos residuales se suma a la distribución de esfuerzos causada por las solicitaciones externas. En general se puede decir que los esfuerzos residuales de tracción disminuyen la resistencia a la fatiga de un elemento, en cambio los esfuerzos residuales por compresión contribuyen a aumentar la duración de la pieza.
b).- Dimensiones y estado superficial de las piezas:
Dimensiones: Se ha comprobado que las propiedades de resistencia mecánica de una pieza, disminuyen a medida que aumenta el tamaño de la misma. Este mismo fenómeno ocurre con la resistencia a la fatiga.
Entallas y concentradores de esfuerzos: estas singularidades o discontinuidades producen aumentos localizados de los esfuerzos, lo que es equivalente a una disminución de las propiedades mecánicas de la pieza en esos puntos.
Terminación superficial: Las irregularidades en la terminación superficial de una pieza, actúan produciendo el efecto de concentradores de esfuerzo.
Temperatura: La temperatura tiene un efecto notable en la resistencia a la fatiga. Piezas sometidas a esfuerzos cíclicos a temperaturas mayores que las ambientales tienen una menor duración.
2.7.2.2.- Resistencia a la fatiga y curva S-N.
La resistencia a la fatiga intrínseca se obtiene en laboratorio bajo las siguientes condiciones:
Ensayo de flexión rotativa.
Superficie pulida a espejo.
Probeta de sección circular de 0.3 pulgadas de diámetro.
Sin presencia de esfuerzos residuales ni concentradores de esfuerzo.
Los niveles de esfuerzos y respectivos ciclos de duración se grafican en un diagrama bilogarítmico, conocido con el nombre de curva S-N o diagrama de Wholer (ver figura 2.17):
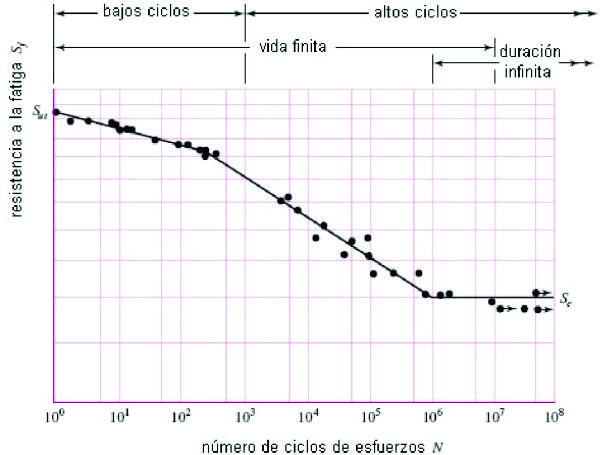
Figura N0 2.18 Típico gráfico de Wholer para la resistencia a la fatiga de un acero: UNSG41300; Sut = 116 kpsi máximo.
Se ha demostrado experimentalmente que los materiales ferrosos pueden resistir un número infinito de ciclos si los esfuerzos están bajo un cierto valor límite de carga. Para un esfuerzo completamente invertido, este valor límite recibe el nombre de límite de resistencia a la fatiga (límite de endurancia).
Haciendo ensayos de fatiga a la flexión para diferentes aceros, se obtuvo una relación empírica entre el valor de la resistencia a la ruptura Sr y el valor límite de resistencia a la fatiga (Sn).
|
[1]
|
En el caso de metales como el aluminio y otras aleaciones no ferrosas, no existe un límite de resistencia a la fatiga definido. Por este motivo, este valor se define para un número de ciclos determinado. Para el Aluminio se considera para N = 5x108 ciclos.
Para el acero este valor se considera para N = 106 ciclos. Dicho valor se modifica en función de los efectos de carga, tamaño y terminación superficial principalmente. De esta forma, la resistencia a la fatiga de una pieza de acero cualquiera, para N = 106 ciclos, está dada por:
|
[2]
|
La figura 2.18 muestra por ejemplo valores para el coeficiente de superficie Cs para distintas calidades en función de la resistencia a la ruptura del acero. Valores para los distintos coeficientes Ci se encuentran en los libros de resistencia de los materiales y/o Mecánica de Sólidos.
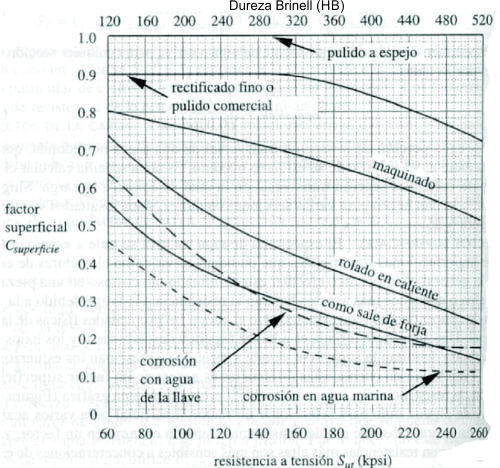
Figura N0 2.19 Coeficiente de superficie.
2.8.- Esfuerzo de Contacto.
La teoría de contactos que permite evaluar los esfuerzos entre las superfiies bajo carga se denomina Teoría de Hertz. El diseño de elementos como los rodamientos y los engranajes generan fuerzas de contacto que esta teoría es capaz de predecir. La Tabla 2.12 mostrada permite determinar los esfuerzos de contacto en cada caso.
Tâbla N0 2.12 Cálculo de esfuerzos de contacto. Teoría de Hertz.
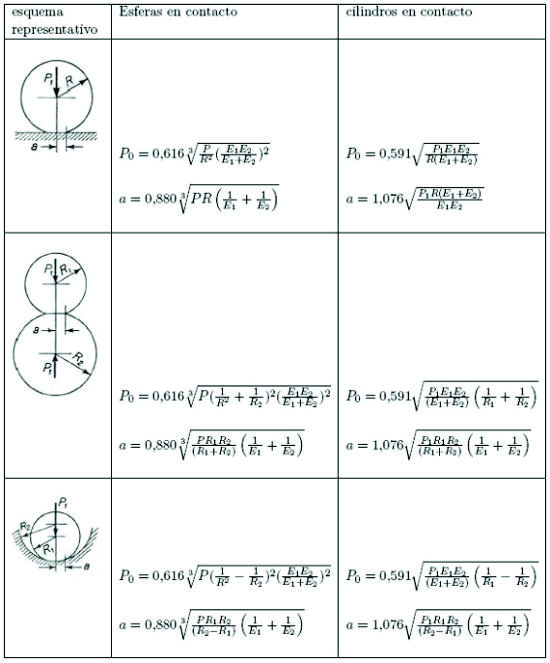
La nomenclatura usada es la siguiente:
P0 |
Máximo esfuerzo de compresión. |
a |
Semi ancho de la zona de contacto. |
P |
Carga total sobre la esfera. |
P1 |
Carga por pulgada axial sobre el cilindro. |
v = 0.3 |
Coeficiente de roce considerado en todos los casos. |
R |
Radio de la esfera o cilindro sobre el plano. |
R1, R2 |
Radios de ambos cilindros o esferas respectivamente. |
E1, E2 |
Módulo de elasticidad de cada cilindro o esfera respectivamente. |
2.9.- Teorías de Falla (Criterios de fluencia y fractura).
En el video, se muestran las cualidades de fallas dúctiles y frágiles en elementos mecánicos simples.
Modos de ruptura en componentes simples. (Recuperado de https://youtu.be/SCtUmppsJKw)
Se entiende por falla aquella situación en que un elemento mecánico ya no puede cumplir de manera satisfactoria con la función para la cual fue creado, ya sea porque se ha deformado plásticamente, se nos ha desgastado o se nos ha fracturado.
Las teorías de falla tratan de describir las condiciones bajo las cuales puede fallar un elemento mecánico. Por lo tanto, la falla de una pieza, implica estados de esfuerzos en un punto que superan la capacidad inherente del material de soportar dichas cargas, así la suposición básica que constituye el marco de referencia para todas las teorías de falla es esto se producirá cuando el esfuerzo principal máximo o el esfuerzo cortante máximo, alcance o supere el valor del mismo parámetro obtenido en una prueba de tensión simple.
A lo largo de los años se han postulado un sin número de teorías de falla, mencionándose a continuación una de las más importantes, así como el tipo de material para el que son valida.
Teoría del Esfuerzo Normal Máximo (Materiales frágiles).
Teoría del Esfuerzo cortante Máximo (Materiales dúctiles).
Teoría de la Energía Máxima de la Distorsión (Materiales dúctiles).
Teoría de Mohr Modificada (Materiales frágiles).
a. Teoría del Esfuerzo Normal Máximo.
Esta teoría establece lo siguiente: la falla de un elemento sometido a un estado multiaxial de esfuerzos se producirá cuando cualquiera de los esfuerzos principales alcance a superar la resistencia máxima del material.
La falla se produce siempre que el mayor esfuerzo principal sea igual a la resistencia de fluencia, o a la resistencia última del material.
Si en un estado de esfuerzo triaxial se tiene que: ![]()
La falla se produce siempre que: ![]()
![]()
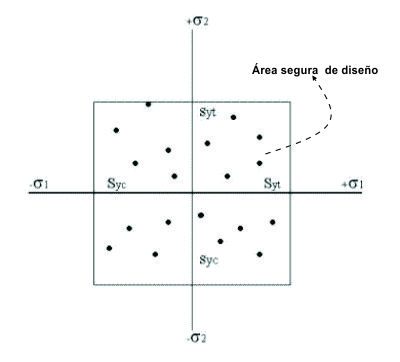
Fig.2.20. Representación gráfica de la teoría del esfuerzo normal máximo. |
Esta teoría expresa que sólo el mayor esfuerzo principal predice falla. Tal predicción no concuerda con los datos experimentales. Sólo los puntos ubicados en el I y el III cuadrante se clasifican como seguros, pero no los puntos ubicados en el II y IV cuadrante. Ver figura 2.20.
|
b. Teoría del Esfuerzo Cortante Máximo
La falla de un elemento sometido a un estado multiaxial de esfuerzos se producirá cuando el esfuerzo cortante producido en la pieza alcance o supere al esfuerzo de corte que se produce en el punto de fluencia de una probeta sometida a una prueba de tensión simple.
De ese modo, se sabe que el esfuerzo cortante máximo (![]() ) producido en un elemento sometido a un estado biaxial de esfuerzos se puede calcular mediante la expresión siguiente:
) producido en un elemento sometido a un estado biaxial de esfuerzos se puede calcular mediante la expresión siguiente:
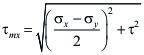
También, con ayuda del círculo de Mohr se puede ver que:
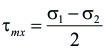
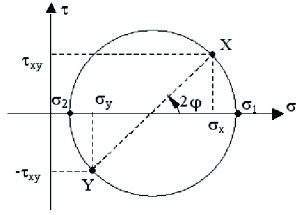
Círculo de Mohr
Por otro lado, se sabe que en una probeta sometida a una carga axial (como en la prueba de tensión), sobre planos a un ángulo de 45º con respecto a los planos perpendiculares a la carga aplicada, se produce un esfuerzo cortante máximo que es igual a la mitad del esfuerzo normal producido, esto es:
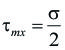
Y cuando se alcanza el punto de fluencia:
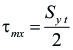
Por lo tanto:
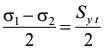
Debiéndose cumplir lo siguiente:
![]()
Debiéndose cumplir con la condición de que ![]() y
y ![]() sean de signos opuestos, esto es, uno debe actuar a compresión y el otro a tensión. En dado caso, que ambos sean a tensión ó ambos a compresión debe satisfacerse lo siguiente:
sean de signos opuestos, esto es, uno debe actuar a compresión y el otro a tensión. En dado caso, que ambos sean a tensión ó ambos a compresión debe satisfacerse lo siguiente:
![]() y
y ![]()
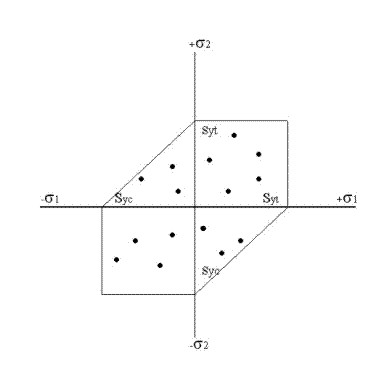
La solución gráfica de esta teoría la desarrolló el ingeniero Paolo Tresca y se muestra en la figura.
Fig. 2.21.- Representación gráfica de la teoría del esfuerzo cortante máximo |
Esta teoría es fácil de emplear y siempre da predicciones seguras con respecto a los resultados de ensayos. se utiliza únicamente para predecir la fluencia y, por lo tanto, sólo se aplica a los materiales dúctiles. Ver figura 2.21.
|
c. Teoría de la Energía Máxima de Distorsión.
Esta teoría fue propuesta por Huber y mejorada posteriormente por Von Mises y Hencky por lo que también se le conoce como criterio de Mises-Hencky.
Esta teoría surgió al observar el comportamiento de los materiales sometidos a cargas hidrostáticas y establece lo siguiente: “La falla de un elemento sometido a un estado multiaxial de esfuerzos se producirá cuando la energía de distorsión por unidad de volumen alcance o supere la energía de distorsión por unidad de volumen que se tiene en el punto de fluencia en una prueba de tensión simple”.
Se puede establecer entonces que la cantidad de energía invertida en deformar un material es el área bajo la curva en el diagrama esfuerzo-deformación de ingeniería (figura 2.22A) y se puede calcular por medio de la ec. siguiente:
![]()
Donde:
Uv = Es la energía que absorbe el material en el cambio de volumen.
Ud = es la energía por cambio de forma (distorsión).
Despejando a Ud se tiene:
![]()
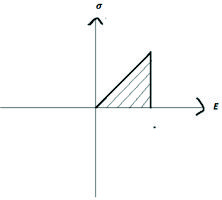
Fig. 2.22A.- Área bajo la curva en el diagrama esfuerzo-deformación de Ingeniería
Para un estado multiaxial de esfuerzos, la energía de distorsión para unidad de volumen, se puede calcular así:
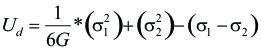
donde G es el modulo de elasticidad al corte y ![]() y
y ![]() son los esfuerzos principales. Para calcular la energía máxima de distorsión por unidad de volumen en le punto de fluencia en una prueba de tensión simple se considera lo siguiente:
son los esfuerzos principales. Para calcular la energía máxima de distorsión por unidad de volumen en le punto de fluencia en una prueba de tensión simple se considera lo siguiente:
![]()
La primera, por que se trata de una prueba de tensión y la segunda condición porque se esta considerando en el punto de fluencia.
Así, Sustituyendo en la ec. se obtiene:
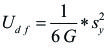
Igualando ambas expresiones se puede establecer que un elemento será seguro siempre y cuando se cumpla lo siguiente:
![]()
Y aplicando un factor de seguridad (n) la ecuación de Von Mises quedaría así.
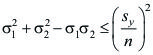
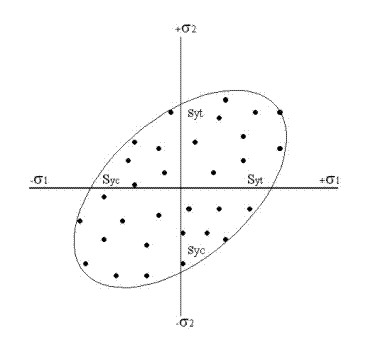
Fig. 2.22 Representación gráfica de la teoría de la energía de la distorsión. |
Esta teoría siempre da predicciones seguras con respecto a los resultados de ensayo. |
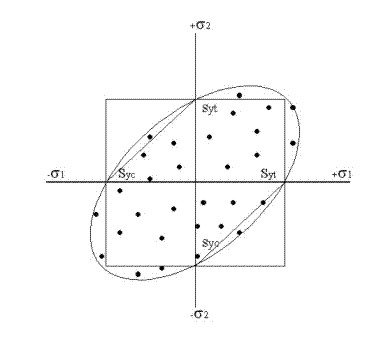
Comparación de las tres Teorías de Esfuerzo:
Figura 2.23.- Representación gráfica de las tres teorías de falla. |
En la figura 2.23, puede observarse el contraste de las tres teorías de falla, la cual revela, para la teoría del esfuerzo normal máximo, inseguridad en las partes superior del cuadrante IV y la parte inferior del cuadrante II. También se observa la elipse inclinada que establece la zona de seguridad de la teoría de la energía de la distorsión y su correspondencia con los resultados experimentales. Por último, la rigidez de la teoría del esfuerzo cortante máximo, que aunque muy segura por su correspondencia con los resultados experimentales, su aplicación se limita sólo a materiales dúctiles. |
d. Teoría de Mohr Modificada.
Esta teoría fue sugerida por el ingeniero alemán Otto Mohr y puede utilizarse para predecir el efecto de un estado biaxial de esfuerzos en un material frágil cuando se encuentran disponibles los resultados de varios tipos de ensayos. Supóngase que a un material frágil se le somete a una prueba de tensión y a una prueba de compresión y apartir de ellos se obtienen la resistencia máxima a tensión (![]() ) y la resistencia máxima a compresión (
) y la resistencia máxima a compresión (![]() ) para dicho material el estado de esfuerzos producido en el punto de esfuerzo máximo se presenta en la figura 2.24A. Para poder analizar el caso cuando
) para dicho material el estado de esfuerzos producido en el punto de esfuerzo máximo se presenta en la figura 2.24A. Para poder analizar el caso cuando ![]() y
y ![]() tienen signos opuestos, se realiza una prueba de torsión y a partir de dicho ensayo se determina la resistencia máxima al corte del material (
tienen signos opuestos, se realiza una prueba de torsión y a partir de dicho ensayo se determina la resistencia máxima al corte del material (![]() ). Dibujando al círculo con centro en el origen del sistema de coordenadas nos representa al estado de esfuerzos correspondiente a la falla en una prueba de torsión.
). Dibujando al círculo con centro en el origen del sistema de coordenadas nos representa al estado de esfuerzos correspondiente a la falla en una prueba de torsión.
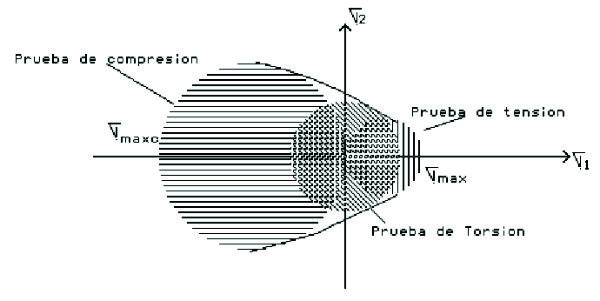
Fig. 2.24A Círculos de Mohr correspondientes a las pruebas de tensión, compresión y torsión.
El criterio de Mohr es lógica extensión de este hecho y de acuerdo con él, un estado de esfuerzos dado es seguro si su representación mediante un círculo éste queda dentro completamente del área limitada por la envolvente de los círculos correspondientes a los datos obtenidos en las distintas pruebas realizadas.
A la teoría de Mohr todavía se le puede hacer un pequeño cambio para ponerla de acuerdo con los resultados experimentales, consiste en extender las líneas del primer y tercer cuadrante dentro del segundo y cuarto como se puede apreciar en la figura 2.22B. Esta teoría se aplica mejor al diseño en forma gráfica.
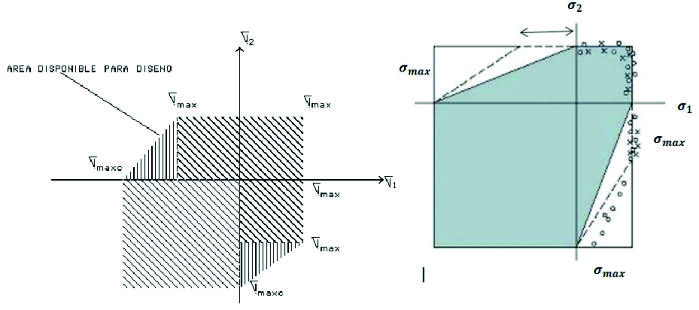
Fig. 2.24B Representación gráfica de la teoría de Mohr Modificada.
En el primer cuadrante debe cumplirse:
![]()
Y en el tercer cuadrante debe cumplirse que:
![]()
Lectura:
Teoría de falla Dinámica - Fatiga.
Análisis de la mecánica de fractura.
2.10.- Coeficientes de seguridad.
Se habla de resistencia de un material cuando se refiere al valor numérico de algún material para el cual se alcanza alguna condición de criticidad. Por ejemplo hablamos de resistencia a la flexión, resistencia a la fatiga, etc. Es común que la mayoía de los autores se refiera a la resistencia de un material con la letra S como símbolo. El valor dado como resistencia de un material siempre se refiere al mínimo valor encontrado experimentalmente.
Adicionalmente siempre existirá en el diseño un grado de incertidumbre sobre los parámetros usados. Entre las incertezas mencionadas en la literatura se pueden considerar a manera de ejemplo:
Composición del material y sus efectos sobre sus características de resistencia.
Falta de homogeneidad que permite que existan zonas de menor resistencia.
Efectos de procedimientos que afectan las superficies, tales como la soldadura.
Aplicación de las cargas (intensidad, zona de aplicación, variabilidad en el tiempo).
Concentradores reales de esfuerzos difíciles de cuantificar.
Efectos de desgaste y corrosión.
Para evaluar la seguridad con que se realiza un cálculo de esfuerzos los autores se refieren al término permisible o admisible (![]() ). Por ejemplo AISC especifica la relación que debe cumplirse entre la resistencia mínima S y el esfuerzo permisible sperm según lo indicado en la tabla siguiente:
). Por ejemplo AISC especifica la relación que debe cumplirse entre la resistencia mínima S y el esfuerzo permisible sperm según lo indicado en la tabla siguiente:
Factores de seguridad según norma AISC
Tensión |
0.45 S0 |
Corte |
|
Flexión |
0.60 S0 |
Aplastamiento |
|
Donde S0 es la resistencia a la fluencia. Norton clasifica en tres categorías las incertidumbres respecto a la seguridad en el diseño, designados como factores F1, F2 y F3 asociados a problemas de material, condiciones de operación y modelos de cargas respectivamente.
Factores de seguridad propuestos por Norton
Información |
Calidad de información |
Factor: F1 |
|
Datos del material disponible de prueba
|
El material realmente utilizado fue aprobado Datos representativos del material disponible a partir de pruebas Datos suficientemente representativos del material disponible a partir de pruebas Datos poco representativos del material disponibles a partir de pruebas |
1.3 2 3
|
Información |
Calidad de información |
Factor: F2 |
|
Condiciones del entorno en el cual se utilizará
|
Idénticas a las condiciones de prueba del material Esencialmente en un entorno de ambiente de habitación Entorno moderadamente agresivo |
1.3 2 3 |
Información |
Calidad de información |
Factor: F3 |
|
Modelos analíticos para carga y esfuerzos
|
Entorno extremadamente agresivo Los modelos han sido probados con experimentos Los modelos representan al sistema con precisión Los modelos representan al sistema sin precisión Los modelos son una burda aproximación. |
1.3 2 3
|
Para materiales dúctiles se trabaja con el mayor valor, es decir, se aplica:
![]()
Para materiales frágiles a menudo se utiliza el doble del valor dado para materiales dúctiles, es decir:
![]()
Respecto a las fuerzas presentes en cualquier problema dado, las normas permiten considerar la mayoría de los efectos reales en función de la siguiente expresión:
![]()
Donde F será la fuerza total usada en el procedimiento de cálculos de la pieza. ![]() Wm es la suma de los pesos muertos (peso de estructura de acero, peso materiales y partes soportantes),
Wm es la suma de los pesos muertos (peso de estructura de acero, peso materiales y partes soportantes), ![]() Wv es el peso de las cargas vivas (peso de equipos, personal, nieve). La consideración de cargas de impacto se realiza amplificando la carga viva Fv por el factor de servicio dado por la tabla siguiente Fw representa las cargas del viento generalmente normalizadas y
Wv es el peso de las cargas vivas (peso de equipos, personal, nieve). La consideración de cargas de impacto se realiza amplificando la carga viva Fv por el factor de servicio dado por la tabla siguiente Fw representa las cargas del viento generalmente normalizadas y ![]() Fdiv representan efectos de terremotos, huracanes o algún tipo de carga de ese tipo.
Fdiv representan efectos de terremotos, huracanes o algún tipo de carga de ese tipo.
Factores de servicio
|
Para soportes de elevadores |
2 |
|
Para vigas maestras de soporte y sus conexiones Para grúas viajeras operadas desde la cabina |
1.25 |
|
Para vigas maestras de soporte y sus conexiones Para grúas viajeras operadas desde el piso |
1.1 |
|
Para para soportes de maquinaria ligera impulsada con eje de transmisión o motor |
|
|
Para soportes de maquinaria de movimiento alternativo o unidades de potencia de impulsión propia |
|
|
Para suspensiones de piso y plataformas |
1.33 |
La forma directa en que se relacionan el esfuerzo presente y la resitencia del material se conocecon el nombre de coeficiente de seguridad, definido como:
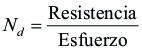
Está ecuación sólo es válida en los casos en que el esfuerzo es linealmente proporcional a la carga. Casos en que ello no se cumpla, se debería utilizar como seguridad estática el valor dado por la siguiente ecuación:

Se acostumbra a diferenciar el factor de seguridad de diseño correspondiente a la intención con que el diseño fue realizado y el factor de seguridad efectivo que corresponde al factor de seguridad que realmente se obtuvo. Es importante destacar que el uso del coeficiente de seguridad debe ser criterioso y todos los valores recomendados en la literatura deberán en la práctica hacerse efectivos basados en la experiencia del diseñador y siempre estableciendo las condiciones de costos involucrados. El mejor ejercicio es realizar un diseño básico y estudiar la influencia del costo del producto variando el coeficiente de seguridad.
Coeficientes de seguridad a la fatiga deben ser siempre mayores que los estáticos y en muchos casos ya está considerado el efecto de cargas dinámicas y/o choqes en el diseño en los valores entregados por la literatura.
Faires entrega valores que se muestran en la siguiente Tabla para que el diseñador tenga una guía respecto a los coeficientes de seguridad.
Coeficientes de seguridad
Clase de carga |
Metales |
Aceros dúctiles |
Hierro fundido, metales quebradizos |
Madera de construcción |
Basado en la reistencia máxima |
Basado en la resistencia de fluencia |
Basado en la resistencia máxima |
Basado en la resistencia máxima |
|
Carga permanente |
3 - 4 |
1.5 - 2 |
5 - 6 |
7 |
Repetida, unidireccional gradual (choque suave) |
6 |
3 |
7 - 8 |
10 |
Repetida, invertida gradual (choque suave) |
5 |
4 |
10 - 12 |
15 |
Choque |
10 15 |
5 - 7 |
15 - 20 |
20 |
|
|