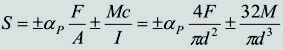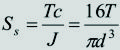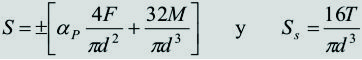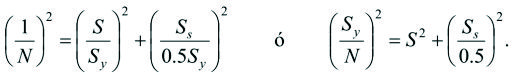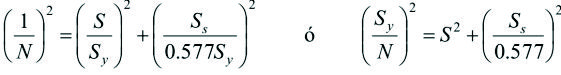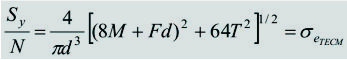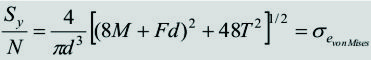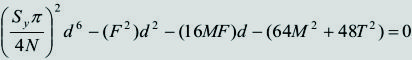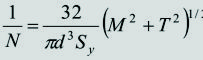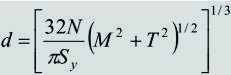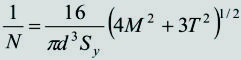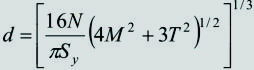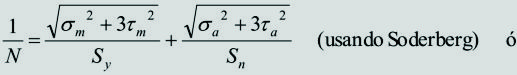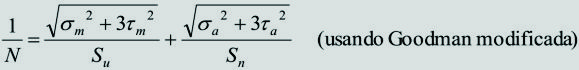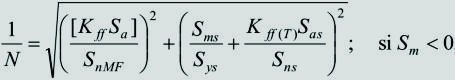Elementos de Máquinas

3.2.- Árboles y Ejes.

1/2 DISEÑO DE EJES | FUERZAS EN ENGRANES | BANDAS | SUJETADORES | DISEÑO MECÁNICO (Recuperado de https://youtu.be/Tq7ECsO9RGQ?si=GywVqJGMEDcdTpEI)

2/2 DISEÑO DE EJES | FUERZAS EN ENGRANES | BANDAS | SUJETADORES | DISEÑO MECÁNICO (Recuperado de https://youtu.be/8H7v-2TFloQ?si=swUwNAJ5lKgiEfLF)

3.2.1.- Introducción.

Sección de árboles o flechas

Geometría de ejes (Recuperado de https://youtu.be/o_PMSTm2DUg)

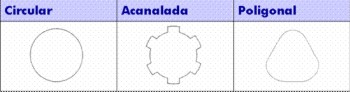
La sección de un árbol de transmisión suele ser circular (maciza o hueca), aunque en ocasiones tiene otras formas como acanalada o poligonal. La forma circular exige el uso de algún elemento de retención circunferencial (chaveta, pasador, prisionero, etc) para evitar el giro de las poleas o engranajes montadas sobre el eje. Las formas acanalada o poligonal permiten obviar el uso de estos elementos ya que proporcionan la retención circunferencial por su propia forma.

a).- Tipo de árboles.

Por la forma del eje geométrico del árbol se distinguen los árboles rectos y los árboles acodados (cigüeñales). Los árboles cigüeñales se emplean siempre que se requiera transformar en una máquina el movimiento alternativo en movimiento giratorio o viceversa. Como se comprenderá, los árboles cigüeñales son característicos de construcciones especiales, lo que hace que los criterios para el dimensionado previo y su cálculo no sean tratados en este curso. También los árboles flexibles con ejes curvilíneos constituyen un grupo especial no tratados en este material.

En cambio la gran difusión de los árboles rectos en la ingeniería mecánica moderna, hace necesario que sean objetos de estudio, con énfasis en el análisis de los criterios de dimensionado previo y de comprobación de la capacidad de carga.

b).- Diferentes tipos de árboles rectos.

c).- Zonas típicas de los árboles.

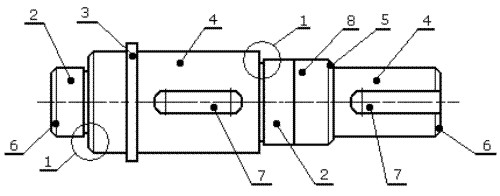
Fig. 3.21

1. Ranura para permitir la salida de la muela de rectificado, o un tallado que requiera diferencia de diámetros entre las secciones contiguas.

2. Muñones de apoyo para los cojinetes de rodamiento o deslizamiento. Pueden ser cilíndricos o cónicos y generalmente son zonas endurecidas superficialmente entre los 48 y 52 HRC. En el caso de muñones para cojinetes de rodamientos debe tenerse en cuenta que su diámetro debe coincidir con la serie de los diámetros de montaje de los rodamientos, usualmente múltiplos de 5.

3. Escalón de apoyo. Sirve para absorber las cargas axiales en los árboles, producto de los elementos que se vinculan a el, y trasmitirlas a los apoyos y anclaje de las máquinas. Otro objetivo, es el garantizar la correcta disposición axial de los elementos en el montaje.

4. Zona de ajuste para el montaje. En caso de no estar en un extremo del árbol, se realiza con un diámetro mayor que las secciones contiguas para permitir el montaje de los elementos. Se recomienda un endurecimiento de la zona entre 48 y 52 HRC.

5. Zona de transición. Son superficies que suavizan los cambios de sección y disminuyen los concentradores de tensión. Suelen ser circulares o elípticas. Es recomendable que sean empleadas superficies con radios mayores al 10 % del diámetro menor de las secciones vinculadas.

6. Biseles. Se emplean para centrar las piezas durante el montaje y también para evitar cortaduras de los operarios durante la manipulación de los árboles.

7. Chaveteros.

8. Zona de centraje. Esta es una zona del árbol contigua a una zona de montaje, con dimensiones ligeramente menores que la de montaje, para facilitar esta operación y el centrado de los elementos.

Los materiales empleados para la construcción de los árboles deben distinguirse por las características de: resistencia suficientemente alta, pequeña sensibilidad a la concentración de tensiones, capacidad de poder ser tratados térmica y químico - térmicamente y poseer buena maquinabilidad.

Tomando lo anterior en consideración es indiscutible que el material más empleado por su excelencia es el acero. Por ello durante este curso serán tratados con exclusividad los árboles rectos de acero, para los cuales se brindan algunas especificidades de los materiales empleados.

d).- El acero como material de árboles y ejes.

La selección de los materiales es una de las partes que integran el diseño de cualquier pieza de las máquinas; en determinados casos no se presta a este asunto toda la atención que merece, y hemos de insistir sobre tan fundamental tema recordando que, antes de decidirse por un material determinado, por sencilla y poca importancia que se le conceda a una pieza a construir, se elija el que reúna las características más apropiadas, no ya solo por su resistencia, sino por su facilidad de maquinado y tratamiento, y muy especialmente también, por el factor económico que puede influir notablemente en el costo de fabricación, por tanto, ha de elegirse el más apropiado con todo detenimiento.

La resistencia y rigidez son factores clave siempre tomados en cuenta en la selección de un material. Igualmente importantes es la confiabilidad relativa y la durabilidad de la pieza cuando se consideran alternativas posibles con respecto al material.

El acero es el material que se usa con más frecuencia para la construcción de los árboles y ejes. Variando adecuadamente la composición, el tratamiento térmico y el tratamiento mecánico pueden obtenerse propiedades mecánicas que se encuentren entre márgenes muy amplios. Para la selección apropiada de la composición del acero son fundamentales tres relaciones básicas:

1. Todos los aceros tienen esencialmente el mismo módulo de elasticidad. Entonces, si el requisito decisivo del árbol o eje es la rigidez, como todos los aceros se comportan igual, debe seleccionarse el de menor costo (incluyendo los costos de fabricación).

2. El contenido de carbono, casi por sí solo, determina la máxima dureza que puede desarrollarse en el acero. El máximo potencial de dureza según el contenido de carbono puede llegar hasta cerca de 0,7%. Esto significa que se puede aplicar un tratamiento térmico a las partes con forma regular, relativamente pequeñas, hechas con acero simple al carbono para obtener esencialmente la misma dureza y resistencia que se lograría con los aceros de aleación más costosa.

3. Los elementos de aleación (manganeso, molibdeno, cromo, níquel y otros) elevan la templabilidad del acero. Por lo tanto, el potencial de dureza y resistencia (el cual está controlado por el contenido de carbono) puede obtenerse con tratamientos térmicos menos drásticos usando dichos elementos de aleación.

Generalmente, los árboles y ejes son hechos de barras circulares de acero al carbón estirado en frío. Son usadas barras de acero aleado cuando se requiere tenacidad, resistencia al impacto y alta resistencia en materiales disponibles de modo comercial. En estos casos, los árboles y ejes pueden tratarse térmicamente para obtener las propiedades requeridas. Cuando la resistencia al desgaste en la superficie es un factor muy importante, puede usarse acero de cierto grado de carburación. Sin embargo, para no aumentar el costo, el diseñador deberá tratar de usar un acero con bajo contenido de carbono, si esto fuera posible, y posteriormente garantizar un endurecimiento local por tratamiento térmico o térmico-químico.

Las barras de acero estiradas en frío tienen las propiedades físicas superiores a las barras estiradas en caliente del mismo material, destacándose una mayor resistencia a la fluencia, a la fractura y a la fatiga. Sin embargo, los valores de fatiga altos a veces son afectados por los esfuerzos residuales de tensión en la superficie que son causados por el estirado en frío.

Prácticamente es aconsejable que las características mecánicas de los aceros sean determinadas por el constructor y/o proveedor, mediante ensayos de los materiales empleados y/o disponibles para la fabricación de los árboles y ejes, con la intención de conocer exactamente los valores limites de resistencia y realizar cálculos precisos de los coeficientes de seguridad.

3.2.2.- Etapas del diseño de árboles.

No hay un riguroso método para llegar al mejor cálculo y diseño de un árbol o un eje, sin embargo se da a continuación una secuencia de cálculo que a consideración del autor es la más racional.

1. Establecer la ubicación relativa de los distintos elementos.
2. Definir el montaje a utilizar para el conjunto, considerando las piezas a colocar, la ubicación y tipo de apoyos no más de dos por tramo. Es recomendable tener en cuenta la forma de armado, mantenimiento y desarmado.
3. Establecer distancias tentativas entre elementos, utilizando un criterio racional.
4. Hallar las reacciones en los apoyos.
5. Realizar los diagramas de esfuerzos actuantes, en los planos correspondientes.
6. Localizar las secciones más solicitadas.
7. Adoptar el material, hacer un precalculo a esfuerzos combinados mediante la fórmula de ASME y un perfilado tentativo.
8. Elegir y dimensionar los elementos de sujeción, chavetas, prisioneros, roscas, etc.
9. Determinar los concentradores de tensiones existentes.
10. Verificar toda la pieza a esfuerzos combinados con cargas de fatiga por flexión alternativa según el método de SODERBERG.
11. Adecuar la pieza a las medidas comerciales y efectuar el perfilado definitivo.
12. Verificar que las deformaciones estén dentro de lo aconsejado de acuerdo al funcionamiento y a los elementos montados, de no ser así redimensionar.

Llegado el caso de que la temperatura de trabajo sea elevada o baja, es necesario efectuar un cálculo particular. Por un lado hay que tener en cuenta el aumento de tensiones y deformaciones (por dilatación o contracción) y además como influye la temperatura en las propiedades del material (tensión de fluencia, resiliencia, tenacidad).

El material más utilizado para árboles y ejes es el acero. Se recomienda seleccionar un acero de bajo o medio carbono, de bajo costo. Si las condiciones de resistencia son más exigentes que las de rigidez, podría optarse por aceros de mayor resistencia.

Es necesario hacer el diseño constructivo al inicio del proyecto, ya que para poder hacer las verificaciones por resistencia, por rigidez y de las frecuencias críticas, se requieren algunos datos sobre la geometría o dimensiones del árbol. Por ejemplo, para verificar la resistencia a la fatiga en una sección determinada es necesario tener información sobre los concentradores de esfuerzos que estarán presentes en dicha sección, así como algunas relaciones entre dimensiones.

El diseño constructivo consiste en la determinación de las longitudes y diámetros de los diferentes tramos o escalones, así como en la selección de los métodos de fijación de las piezas que se van a montar sobre el árbol. En esta etapa se deben tener en cuenta, entre otros, los siguientes aspectos:

• Fácil montaje, desmontaje y mantenimiento.
• Los árboles deben ser compactos, para reducir material tanto en longitud como en diámetro (recuérdese que a mayores longitudes, mayores tenderán a ser los esfuerzos debidos a flexión y, por lo tanto, los diámetros).
• Permitir fácil aseguramiento de las piezas sobre el árbol para evitar movimientos indeseables.
• Las medidas deben ser preferiblemente normalizadas.
• Evitar discontinuidades y cambios bruscos de sección, especialmente en sitios de grandes esfuerzos.
• Generalmente los árboles se construyen escalonados para el mejor posicionamiento de las piezas.
• Generalmente los árboles se soportan sólo en dos apoyos, con el fin de reducir problemas de alineamiento de éstos.
• Ubicar las piezas cerca de los apoyos para reducir momentos flectores.
• Mantener bajos los costos de fabricación.
• Basarse en árboles existentes o en la propia experiencia, para configurar el árbol (consultar catálogos y analizar reductores y sistemas de transmisión de potencia).

Después del diseño constructivo puede procederse a verificar la resistencia del árbol. Los árboles deben tener la capacidad de soportar las cargas normales de trabajo y cargas eventuales máximas, durante la vida esperada. Entonces, se debe verificar la resistencia del árbol a la fatiga y a las cargas dinámicas; estas últimas son generalmente las cargas producidas durante el arranque del equipo.

Debe hacerse también un análisis de las frecuencias naturales (críticas) del árbol. Todo sistema tiende a oscilar con una gran amplitud cuando se excita con determinadas frecuencias; esto se denomina resonancia. Los árboles, junto con las piezas que se montan sobre ellos, tienden también a vibrar excesivamente cuando giran a las velocidades críticas. El diseñador debe asegurar que la velocidad de rotación del árbol sea bastante diferente de cualquier velocidad que produzca resonancia; de lo contrario, las deflexiones o deformaciones del árbol tenderían a ser grandes y a producir la falla.

Finalmente, los árboles deben tener suficiente rigidez, con el objetivo de evitar que las deformaciones excesivas perjudiquen el buen funcionamiento de las piezas que van montadas sobre éstos. Por ejemplo, deformaciones excesivas en los árboles pueden hacer que el engrane de un par de ruedas dentadas no sea uniforme o no se extienda en toda la altura de trabajo del diente. Por otro lado, los cojinetes (de contacto rodante o deslizante) se pueden ver afectados si las pendientes del árbol en los sitios de los cojinetes son muy grandes. Como los aceros tienen esencialmente igual módulo de elasticidad, la rigidez de los árboles debe controlarse mediante decisiones geométricas.

En conclusión, el buen funcionamiento de un árbol depende de muchos factores, entre los cuales podemos mencionar una buena resistencia y rigidez, una correcta fijación de las piezas, una adecuada alineación y lubricación de los elementos que lo requieran.

3.2.2.1 Resistencia de los ärboles.

Estimación de esfuerzos en ejes (Recuperado de https://youtu.be/7wrvxRHGJSs)

Criterios de combinación de esfuerzos en ejes (Recuperado de https://youtu.be/Ujj236TjMAQ)

Diagramas de carga (Recuperado de https://youtu.be/mGeeAoNNweQ)

Criterios de falla (Recuperado de https://youtu.be/yi3Bxgy28HE)

Proceso de diseño y ejemplo de cálculo (Recuperado de https://youtu.be/rTwMQpIwLzA)

Ejemplo de cálculo de resistencia de un eje para un reductor de dos etapas (Recuperado de https://youtu.be/FkeNTrASUvE)

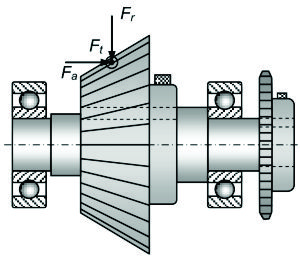
a) Resistencia de los árboles. - Los elementos de transmisión de potencia como las ruedas dentadas, poleas y estrellas transmiten a los árboles fuerzas radiales, axiales y tangenciales. Debido a estos tipos de carga, en el árbol se producen generalmente esfuerzos por flexión, torsión, carga axial y cortante. La figura muestra esquemáticamente un árbol en el cual está montado un engranaje cónico y una estrella. Se muestran las fuerzas sobre el engranaje, las cuales producen los cuatro tipos de solicitación mencionados.

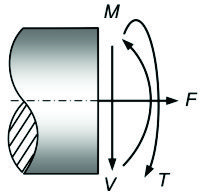
Como se muestra en la figura, en cualquier sección transversal de un árbol existe, en general, un par de torsión, T, una carga axial, F, una fuerza cortante, V, y un momento flector, M. Estas cargas producen los esfuerzos siguientes:

• Esfuerzos cortantes producidos por el par de torsión. Si la sección es circular sólida, los puntos de mayor esfuerzo cortante son los ubicados en la periferia, y dicho esfuerzo, Ss, está dado por:

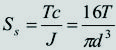  [1]

  donde T, c, J y d son el par de torsión, la distancia desde el eje neutro hasta los puntos de mayor esfuerzo, el momento polar de inercia y el diámetro, respectivamente, de la sección transversal que se esté analizando.

• Esfuerzos normales por carga axial. El esfuerzo normal, S_F, es constante en toda la sección y está dado por:

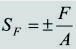  [2]

  donde F y A son la fuerza axial y el área transversal, respectivamente, de la sección de análisis. El signo '+' indica que el esfuerzo es de tracción y se toma si F es de tracción; el signo '–' se toma si F es de compresión.

  Cuando la carga es de compresión, la ecuación anterior es válida si no existe posibilidad de pandeo. Si el árbol es 'esbelto', una carga de compresión puede tratar de flexionarlo (pandearlo), produciéndose esfuerzos por carga axial y flexión combinadas. Como el esfuerzo máximo en una columna esbelta es mayor que el dado por la ecuación [2], debemos utilizar una ecuación diferente. Faires propone calcular un esfuerzo equivalente, S_eF (que es diferente al esfuerzo real máximo) para el caso de columnas:

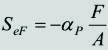  [3]

  donde 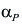es un coeficiente mayor o igual a la unidad que tiene en cuenta el efecto de pandeo y se calcula de maneras diferentes de acuerdo con el tipo de columna (esbelta, corta, de esbeltez media)

  Nota.- La esbeltez de una columna está dada por la relación entre su longitud, L, y el radio de giro, k, de la sección transversal; este último es igual a la raíz cuadrada de la relación entre el menor momento rectangular de inercia de la sección y el área: k = (I/A)^1/2.

  El coeficiente 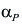está dado, por ejemplo, por:

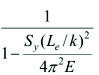  [para la fórmulade Johnson]

  o

  [parala ecuación de Euler]

  donde Le es la longitud libre efectiva de la columna.

• Esfuerzos normales producidos por el momento flector. El esfuerzo normal, S_M, es máximo en las fibras más alejadas del eje neutro y está dado por:

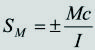  [4]

  donde M, c e I son el momento flector, la distancia desde el eje neutro hasta las fibras más alejadas y el momento rectangular de inercia, respectivamente, de la sección de análisis. El signo '+' se toma si el punto analizado está a tracción y el signo '–' si está a compresión. En general, existirán dos valores de c, uno para los puntos a tracción y otro para los puntos a compresión.

  Algunas veces se tienen dos componentes del momento flector, Mxy y Mxz, donde x es la dirección axial y y y z son direcciones cartesianas paralelas a la sección del árbol. Como generalmente interesa el momento resultante, éste se puede obtener mediante:

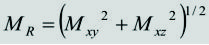  [5]

  Nótese que las componentes Mxy y Mxz son perpendiculares entre sí, por lo que el momento resultante se obtiene utilizando el teorema de Pitágoras, dado por la ecuación anterior.

• Esfuerzos cortantes producidos por la fuerza cortante, V. Normalmente, estos esfuerzos son mucho más pequeños que, por ejemplo, los esfuerzos normales debidos a flexión y tienden a actuar en puntos donde otros esfuerzos son pequeños o son iguales a cero. Debido a esto, es práctica común no tener en cuenta el efecto de la fuerza cortante, aunque si ésta se considera suficientemente grande, debe tenerse en cuenta este efecto.

Adicionalmente, pueden existir esfuerzos de compresión transversales al árbol cuando existen ajustes de interferencia, llamados también ajustes forzados. Aunque los esfuerzos de compresión tienden a inhibir la fatiga, éstos pueden provocar fluencia en el árbol cuando actúan las cargas dinámicas (cargas pico). Los esfuerzos producidos por ajustes de interferencia podrían despreciarse en el diseño, si las interferencias son 'pequeñas'.

Teniendo en cuenta lo estudiado en los capítulos anteriores, se concluye que el punto o puntos críticos de cualquier sección transversal tienen estados de esfuerzo como el de la figura. Entonces, el estado de esfuerzo es biaxial, donde uno de los esfuerzos normales es igual a cero.

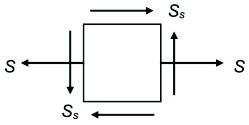
Estado de esfuerzo usual de los puntos críticos de un árbol

Para árboles de sección circular sólida, los esfuerzos S y Ss de la figura anterior están dados por:

El valor de es igual a uno si la fuerza F es de tracción. Para otros tipos de secciones se deben usar las ecuaciones que correspondan.

La determinación de la sección o secciones críticas se basa parcialmente en estas ecuaciones. De acuerdo con éstas, la sección es más crítica si:

• Su diámetro es pequeño.
• Las cargas F, M y T son grandes.
• Adicionalmente, por el criterio de fatiga, una sección es más crítica en la medida en que tenga discontinuidades, gran rugosidad superficial, etc..

Como generalmente no existe una sección en la cual las propiedades seccionales sean menores y las cargas sean mayores, etc., deben analizarse las secciones críticas de los diferentes tramos del árbol. No necesariamente la sección crítica es aquella en la cual alguna carga es máxima o alguna propiedad es mínima, ya que alguna combinación de propiedades y cargas sub-críticas podría ser la más crítica. Debe tenerse un cuidado similar al escoger los puntos críticos (de las secciones críticas), si no existe un punto en el cual actúen simultáneamente los esfuerzos máximos por carga axial, flexión y torsión.

Nota.- Para otro tipo de secciones y cargas complejas, esta parte no se debe tomar en cuenta.

b) Análisis estático de árboles dúctiles uniformes de sección transversal circular sólida. - El análisis estático de un árbol consiste en verificar que éste no fallará inmediatamente después de aplicar ciertas cargas. Este análisis podría efectuarse para:

1. Comprobar su resistencia “estática” a las cargas nominales. Esto es poco usual ya que debe verificarse la resistencia a la fatiga de los árboles (las ecuaciones de fatiga cubren también las fallas “estáticas”).
2. Comprobar su resistencia estática a las cargas dinámicas (cargas pico). Esta comprobación sí debe hacerse ya que normalmente en los arranques o cuando hay sobrecargas, los árboles están sometidos a esfuerzos mayores a los nominales. Como se prevé que estas cargas se repiten un número muy pequeño de veces, éstas no tenderían a producir falla por fatiga, siendo suficiente el análisis de diseño estático.

En un diseño para cargas estáticas, se aplica una teoría de falla estática adecuada al punto o puntos más críticos del árbol, los cuales tienen estados de esfuerzo como el de la figura anterior y esfuerzos dados por las ecuaciones [6] y [7], si la sección es circular sólida.

Como en su gran mayoría los árboles se fabrican con barras circulares de materiales dúctiles y uniformes (resistencia a la tracción igual a la de compresión), plantearemos las ecuaciones de diseño para árboles con estas características. Para un árbol dúctil y uniforme de sección transversal circular sólida, las ecuaciones [6] y [7] se pueden expresar como:

Nótese que para S se toman, de la ecuación [6], ya sea los dos signos positivos o los dos negativos; la razón de esto es que el punto crítico de un árbol de sección circular y material uniforme es aquel en el cual actúa el esfuerzo normal máximo, es decir, en donde se suman los esfuerzos por carga axial y por flexión. No importa si el esfuerzo resultante es de tracción o de compresión, ya que la resistencia estática de un material uniforme es igual para estos dos tipos de esfuerzo.

A un material dúctil se le aplica la Teoría del Esfuerzo Cortante Máximo (TECM) o la teoría de von Mises-Hencky (teoría de la energía de distorsión), la cual es equivalente a la Teoría del Esfuerzo Cortante Octaédrico (TECO). Las ecuaciones de diseño de estas teorías, para el estado de esfuerzo de nuestro punto crítico (figura anterior), están dadas por:

TECM

TECO/von Mises

Reemplazando las ecuaciones [8] (con = 1) en las ecuaciones anteriores y organizando se obtiene:

TECM

Para la TECO/von Mises

Nótese que los términos intermedios en las ecuaciones [11] y [13] están igualados a Sy/N; por lo tanto, corresponden a los esfuerzos equivalentes de las teorías. Las ecuaciones [11] a [14] tienen, entre otras, las siguientes condiciones:

• El análisis es de diseño estático.
• El material es dúctil y uniforme.
• El punto crítico no tiene esfuerzos producidos por cortante directo ni por ajustes de interferencia.
• La sección a analizar es circular sólida.
• Si la sección de análisis está sometida a compresión, no existe posibilidad de pandeo en dicha sección. En caso de pandeo, el esfuerzo no es proporcional a la fuerza de compresión y los factores de seguridad calculados con las ecuaciones no serían correctos (nótese que el término 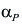de la ecuación [8] se ha omitido en las ecuaciones de diseño).

Los signos de la ecuación [8] no aparecen en las ecuaciones anteriores, debido a que el esfuerzo S está elevado al cuadrado. Entonces, se debe tener en cuenta que los valores de M y F se toman siempre positivos, independientemente de si producen tracción o compresión en el punto y, por supuesto, de si en el diagrama de momento M es negativo o positivo.

Si además de las condiciones anteriores, no existe fuerza axial en la sección de análisis (F = 0), las ecuaciones [11] a [14] se reducen a:

Para la TECM

Para la TECO/von Mises

Como se dijo anteriormente, las ecuaciones de diseño para cargas estáticas se usan normalmente para la verificación de la resistencia a las cargas pico. En este caso, M, T y F serían las cargas pico máximas, y no las cargas normales de trabajo. Si el factor de seguridad calculado con la ecuación [11], [13], [15] ó [17] es muy pequeño (menor que el admisible), debe rediseñarse el árbol calculando un nuevo diámetro con la ecuación [12], [14], [16] ó [18]. En el siguiente ejemplo se ilustra la aplicación del análisis estático de árboles.

c) Análisis por fatiga de árboles dúctiles

Introducción.- Como se dijo, los árboles soportan cargas variables y, por lo tanto, debe comprobarse su resistencia a la fatiga. Por ejemplo, unas cargas constantes T, M y F en un árbol, producen esfuerzos normales variables, ya que el momento flector M es giratorio relativo a un observador parado en un punto del árbol rotativo (figura siguiente). Eventualmente, en caso de no tener la suficiente información para efectuar el diseño por fatiga, un análisis de diseño estático podría reemplazarlo, si se usa un factor de seguridad bastante grande; sin embargo, este último diseño no garantiza la duración requerida del árbol.

Un par flector constante en magnitud y dirección produce esfuerzos variables, ya que el árbol gira.

En este capítulo nos limitaremos al análisis de árboles cuyos puntos críticos tengan estados de esfuerzo como el de la figura anterior (estado de esfuerzo biaxial con un solo esfuerzo normal y un esfuerzo cortante). Este tipo de estado de esfuerzo se obtiene en las secciones de los árboles en las que no existan ajustes con interferencia (o si existen, los esfuerzos son tan pequeños que no es necesario tenerlos en cuenta), y que además no existan (o sean despreciables) esfuerzos producidos por fuerzas cortantes. Esto último no es problema, ya que es práctica común no tener en cuenta los esfuerzos producidos por estas fuerzas.

Estado de esfuerzo de los puntos críticos de un árbol, cuando no se tienen en cuenta o no existen esfuerzos producidos por cortante directo y por ajustes forzados

A continuación se presentan tres métodos para el análisis por fatiga de árboles con puntos críticos como el mostrado en la figuraanterior. El método von Mises (estudiado en el capítulo 5), el método adoptado por Faires y el método ASME.

Método von Mises

Teniendo en cuenta que uno de los esfuerzos normales, , es cero

donde los esfuerzos pueden calcularse así:

Los subíndices (T), (F) y (M) para los factores Kfm y Kff indican que éstos corresponden a torsión, carga axial y flexión, respectivamente. Los esfuerzos S_m(F) y S_a(F) son las componentes media y alternativa del esfuerzo producido por la fuerza axial, y los esfuerzos S_m(M) y S_a(M) son las componentes media y alternativa del esfuerzo producido por flexión. Nótese que no es necesario verificar la condición de resistencia estática, si se verifica la resistencia del árbol a las cargas dinámicas.

Este método puede utilizarse para el diseño de árboles que cumplan las siguientes condiciones en el punto a analizar:

• Material dúctil o frágil.
• Los esfuerzos normal y cortante varían en fase y con la misma frecuencia (los esfuerzos alcanzan sus valores máximos al mismo tiempo, al igual que sus valores mínimos). Sin embargo, podría utilizarse si esto no se cumple. Se espera que en la mayoría de los casos los resultados sean conservadores.
• El estado de esfuerzo es como el de la figura anterior; para lo cual los esfuerzos debidos a ajustes de interferencia y a fuerzas cortantes, si los hay, son despreciables.
• Si la sección de análisis está sometida a compresión, no existe posibilidad de pandeo del árbol en dicha sección.

Método adoptado por Faires

La ecuación siguiente es una variante de la propuesta por Faires