3.2.- Selección de Rodamientos
Selección de Rodamientos y Cálculo de Vida (Recuperado de https://youtu.be/euKh6-U-rMk)
Ver: Proceso de selección de rodamientos SKF
Selección de Rodamientos solicitadas dinámicamente a base de Catalogo SKF, se basa en el análisis de los principales parámetros de funcionamiento y las exigencias del usuario. Estos parámetros pueden ser:
|
|
El proceso ofrece un enfoque sencillo paso a paso, que muestra la relación general entre cada paso. Al definir y nombrar claramente los pasos de esta manera, debería resultar más fácil encontrar información sobre un tema específico. En realidad, sin embargo, encontrará interdependencias que requieren saltar de un paso a otro sin un orden estricto.
3.2.1.- Selección del tipo de rodamiento.
Cada tipo de rodamiento presenta propiedades características que dependen de su diseño y que lo hacen más o menos adecuado para una aplicación determinada. Por ejemplo, los rodamientos rígidos de bolas pueden soportar cargas radiales moderadas, así como cargas axiales. Tienen una baja fricción y pueden ser fabricados con una gran precisión y con un diseño de funcionamiento silencioso. Por tanto, estos rodamientos son los preferidos para los motores eléctricos de tamaño pequeño y mediano.
Los rodamientos CARB y de rodillos a rótula pueden soportar cargas muy elevadas y son autoalineables. Estas propiedades hacen que sean especialmente adecuados, por ejemplo, para aplicaciones de ingeniería pesada, donde existen cargas muy elevadas, y flexiones del eje y desalineaciones.
En muchos casos, sin embargo, se deben considerar diversos factores y contrastarlos entre sí a la hora de seleccionar un tipo de rodamiento, por tanto, no es posible dar unas reglas generales.
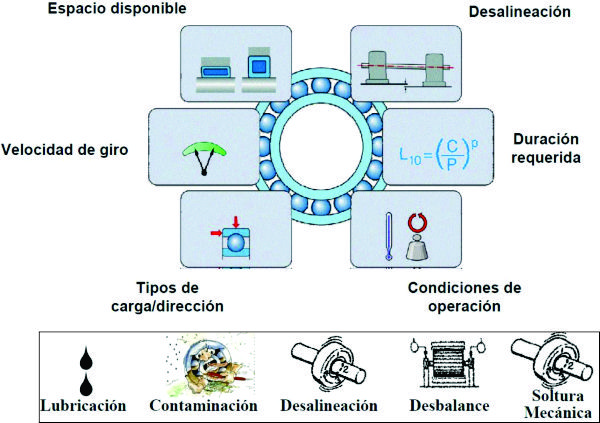
La información facilitada a continuación, debe servir para indicar los puntos más importantes a considerar a la hora de seleccionar un tipo de rodamiento estándar, y facilitar así una elección apropiada:
Espacio disponible
Cargas
Desalineación
Precisión
Velocidad
Funcionamiento silencioso
Rigidez
Desplazamiento axial
Montaje y desmontaje
Obturaciones integrales
Las recomendaciones que se dan a continuación, le pueden ser de utilidad:
3.2.1.1.- Espacio disponible
En muchos casos, una de las dimensiones principales del rodamiento, el diámetro del agujero, viene determinado por las características de diseño de la máquina y por el diámetro del eje.
Para los ejes de diámetro pequeño, se puede utilizar cualquier tipo de rodamiento de bolas, siendo los rodamientos rígidos de bolas los más utilizados; los rodamientos de agujas también son adecuados (Fig 1). Para ejes de diámetros grandes, se pueden considerar los rodamientos de rodillos cilíndricos, cónicos, a rótula y CARB, así como los rodamientos rígidos de bolas (Fig 2).
Fig. 1
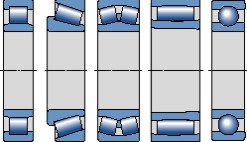
Fig. 2
Cuando el espacio radial disponible es limitado, se deberán seleccionar rodamientos de sección pequeña, particularmente los de baja altura de sección, es decir, los rodamientos de la serie de diámetros 8 o 9 (ver "Dimensiones" en la sección "Datos de los rodamientos - general"). Las coronas de agujas, los casquillos de agujas y los rodamientos de agujas con o sin aro interior (Fig 3), son muy adecuados, así como determinadas series de rodamientos rígidos de bolas, de bolas con contacto angular, rodamientos de rodillos cilíndricos, cónicos, a rótula y CARB.
Cuando el espacio axial es limitado, para cargas radiales y combinadas, se pueden usar algunas series de rodamientos de rodillos cilíndricos y de rodamientos rígidos de bolas respectivamente (fig 4) así como los diversos tipos de rodamientos de agujas combinados (fig 5). Para las cargas puramente axiales se pueden usar coronas axiales de agujas (con o sin arandelas), así como rodamientos axiales de bolas y rodamientos axiales de rodillos cilíndricos (fig 6).
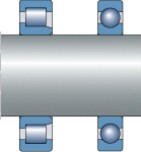
Fig. 4
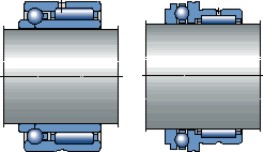
Fig. 5
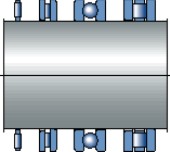
Fig. 6

Fig. 3
3.2.1.2.- Cargas
a).- Magnitud de la carga.
La magnitud de la carga es uno de los factores que suele determinar el tamaño del rodamiento a utilizar. Por lo general, los rodamientos de rodillos pueden soportar mayores cargas que los rodamientos de bolas de tamaño similar (fig 7) y los rodamientos llenos de elementos rodantes, sin jaula pueden soportar mayores cargas que los rodamientos con jaula correspondientes. Los rodamientos de bolas son los más utilizados cuando las cargas son ligeras o moderadas. Para cargas elevadas y ejes de grandes diámetros, la elección mas adecuada son los rodamientos de rodillos.
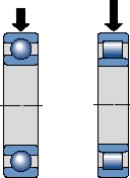
Fig. 7
b).- Sentido de la carga.
Los rodamientos de rodillos cilíndricos de tipo NU y N, los rodamientos de agujas y los rodamientos CARB sólo pueden absorber cargas puramente radiales (fig 8). Todos los demás rodamientos radiales pueden absorber algunas cargas axiales además de las cargas radiales; ver "Cargas combinadas".
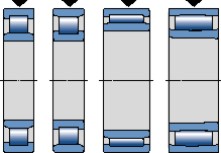
Fig. 8
Los rodamientos axiales de bolas y los rodamientos de bolas con cuatro puntos de contacto (fig 9) son adecuados para las cargas puramente axiales ligeras o moderadas. Los rodamientos rígidos de bolas de simple efecto sólo pueden soportar cargas axiales en un sentido; para las cargas axiales en ambos sentidos, son necesarios los rodamientos rígidos de bolas de doble efecto.
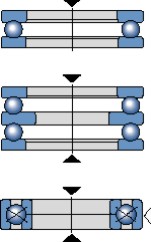
Fig. 9
Los rodamientos axiales de bolas con contacto angular pueden soportar cargas axiales moderadas a altas velocidades; en estos casos los rodamientos de simple efecto también pueden soportar cargas axiales simultáneas, mientras que los rodamientos de doble efecto se usan normalmente para cargas puramente axiales (fig 10).
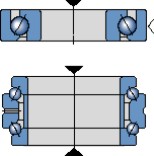
Fig. 10
Para las cargas axiales moderadas y elevadas en un sentido, los rodamientos más adecuados son los rodamientos axiales de agujas y los rodamientos axiales de rodillos cilíndricos y cónicos, así como los rodamientos axiales de rodillos a rótula (fig 11). Los rodamientos axiales de rodillos a rótula también pueden soportar cargas radiales simultáneas. Para las cargas axiales alternas elevadas, se pueden montar dos rodamientos axiales de rodillos cilíndricos o de rodillos a rótula adyacentes entre sí.
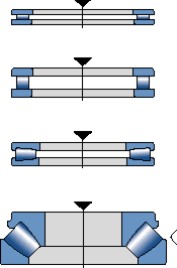
Fig. 11
Una carga combinada consta de una carga radial y una carga axial que actúan simultáneamente. La capacidad que tiene un rodamiento para soportar una carga axial está determinada por su ángulo de contacto
 ; cuanto mayor es dicho ángulo, más adecuado es el rodamiento para soportar cargas axiales. El factor de cálculo Y, que disminuye al aumentar el contacto
; cuanto mayor es dicho ángulo, más adecuado es el rodamiento para soportar cargas axiales. El factor de cálculo Y, que disminuye al aumentar el contacto  , proporciona una indicación exacta. Los valores de este factor para un tipo de rodamiento o para los rodamientos individuales podrán encontrarse en el texto introductorio de las secciones de las tablas de rodamientos, o en las propias tablas de rodamientos. La capacidad de carga axial de los rodamientos rígidos de bolas depende de su diseño interno y del juego interno del rodamiento.
, proporciona una indicación exacta. Los valores de este factor para un tipo de rodamiento o para los rodamientos individuales podrán encontrarse en el texto introductorio de las secciones de las tablas de rodamientos, o en las propias tablas de rodamientos. La capacidad de carga axial de los rodamientos rígidos de bolas depende de su diseño interno y del juego interno del rodamiento.Para las cargas combinadas, se usan principalmente los rodamientos de una hilera y de dos hileras de bolas con contacto angular y los rodamientos de una hilera de rodillos cónicos, aunque los rodamientos rígidos de bolas y los rodamientos de rodillos a rótula también son adecuados (fig 12). Asimismo, los rodamientos de bolas a rótula y los rodamientos de rodillos cilíndricos de tipo NJ y NUP, así como los rodamientos de rodillos cilíndricos de tipo NJ y UN con aro angular HJ, también se pueden utilizar para las cargas combinadas con un componente axial relativamente pequeño (fig 13).
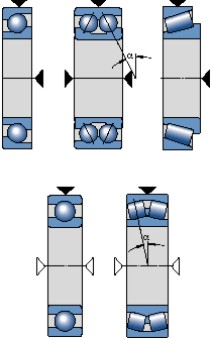
Fig. 12
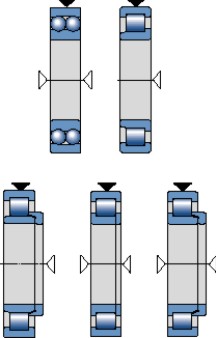
Fig. 13
Los rodamientos de una hilera de bolas con contacto angular, los rodamientos de rodillos cónicos, los rodamientos de rodillos cilíndricos de tipo NJ y UN+HJ y los rodamientos axiales de rodillos a rótula, sólo pueden soportar cargas axiales en un sentido. Para las cargas alternantes, estos rodamientos se deben combinar con un segundo rodamiento. Por esta razón, los rodamientos de una hilera de bolas con contacto angular están disponibles como "rodamientos universales" para un montaje apareado, y además se pueden suministrar rodamientos de una hilera de rodillos cónicos emparejados.
Cuando el componente axial de las cargas combinadas es elevado, éste se puede soportar de forma independiente de la carga radial por un rodamiento independiente. Además de los propios rodamientos axiales, existen algunos rodamientos radiales, como los rodamientos rígidos de bolas o los rodamientos rígidos de bolas con cuatro puntos de contacto (fig 14a) que son adecuados para esta tarea. En estos casos, para tener la seguridad de que el rodamiento sólo se somete a la carga axial, el aro exterior del rodamiento se debe montar con un juego radial. (fig 14b).
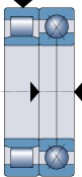
Fig. 14a
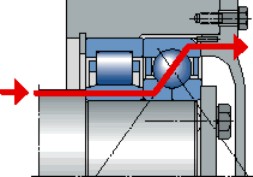
Fig. 14b
Cuando una carga actúa excéntricamente sobre un rodamiento, se puede producir un par de inclinación. Los rodamientos de dos hileras, por ejemplo los rodamientos rígidos de bolas o de bolas con contacto angular, pueden soportar pares de inclinación, pero son más adecuados los rodamientos de una hilera de bolas con contacto angular emparejados o los rodamientos de rodillos cónicos en una disposición cara a cara, o mejor aún, espalda con espalda (fig 15).
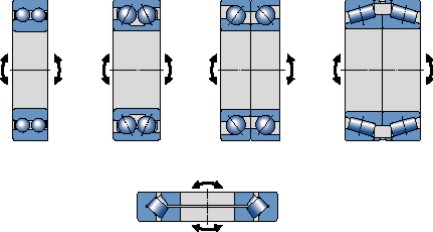
Fig. 15
i).- Carga radial.
ii).- Carga axial.
iii).- Carga combinada.
4i).- Carga de momento.
c).- Desalineación
Las desalineaciones angulares entre el eje y el soporte se pueden originar, por ejemplo, flexión del eje bajo la carga de funcionamiento, cuando los asientos en el soporte no están mecanizados a la misma altura o cuando los ejes están soportados por rodamientos montados en soportes distintos y a gran distancia entre sí.
Los rodamientos rígidos, es decir los rodamientos rígidos de bolas y los rodamientos de rodillos cilíndricos, no pueden soportar ninguna desalineación, o sólo desalineaciones muy pequeñas, a no ser que se fuercen. Por otra parte, los rodamientos autoalineables, es decir, los rodamientos de bolas a rótula, los rodamientos de rodillos a rótula, los rodamientos CARB y los rodamientos axiales de rodillos a rótula (fig 16), pueden soportar las desalineaciones producidas bajo las cargas de funcionamiento y también pueden compensar los errores de alineación iniciales producidos por errores de mecanización o de montaje. Los valores permisibles para las desalineaciones figuran en el texto introductorio de la sección de la tabla correspondiente.
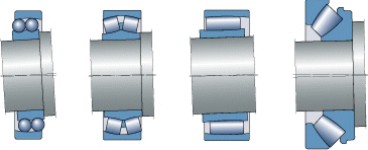
Fig. 16
Los rodamientos axiales de bolas con arandelas de alojamiento esféricas y aros de asiento, las unidades Y y los rodamientos de agujas (fig 17) pueden compensar la desalineación inicial debida a errores de mecanización o de montaje.
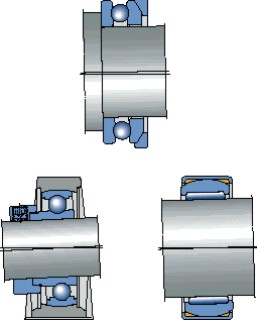
Fig. 17
d).- Ajustes y Tolerancias
Ajustes y Tolerancias (Recuperado de https://youtu.be/4geKV88hWa0)
3.2.1.3.- Precisión
Para las aplicaciones que requieren una alta precision de funcionamiento y altas velocidades, se requieren rodamientos con una precisión mayor que la Normal, por ejemplo, disposiciones de husillos para máquinas herramientas.
Los textos introductorios de cada tabla contienen información acerca de las clases de tolerancia según las cuales se fabrican los rodamientos de esa sección. SKF fabrica una amplia gama de rodamientos de alta precisión, entre los que se incluyen los rodamientos de una hilera de bolas con contacto angular, los rodamientos de una hilera y de dos hileras de rodillos cilíndricos y los rodamientos axiales de bolas con contacto angular de simple o doble efecto, ver el catálogo de SKF "High-precision bearings" (Rodamientos de alta precision).
3.2.1.4.- Velocidad
La temperatura de funcionamiento permitida limita la velocidad a la que los rodamientos pueden funcionar. Los rodamientos que ofrecen una baja fricción y por tanto una baja generación de calor dentro del rodamiento son los más apropiados para el funcionamiento a alta velocidad.
Las velocidades más altas se pueden alcanzar con los rodamientos rígidos de bolas y con los rodamientos de bolas a rótula cuando las cargas son puramente radiales y con los rodamientos de bolas con contacto angular para cargas combinadas. Esto es particularmente cierto de los rodamientos de bolas con contacto angular de alta precisión o de los rodamientos rígidos de bolas con elementos rodantes cerámicos.
Debido a su diseño, los rodamientos axiales no pueden soportar velocidades tan altas como los rodamientos radiales.
3.2.1.5.- Funcionamiento silencioso
En ciertas aplicaciones, p.ej. pequeños motores eléctricos para electrodomésticos o equipos de oficina, el ruido producido durante el funcionamiento es un factor importante y puede influir en la elección de un rodamiento. Los rodamientos rígidos de bolas SKF, se fabrican especialmente para este tipo de aplicaciones (fig 18).

Fig. 18
3.2.1.6.- Rigidez
La rigidez de un rodamiento se caracteriza por la magnitud de la deformación elástica (resiliencia) del rodamiento cargado. Normalmente, esta deformación es muy pequeña y puede ser ignorada. En algunos casos, por ejemplo en los husillos para máquinas herramienta o en disposiciones de rodamientos de piñón, la rigidez es un factor importante.
Debido al contacto entre los elementos rodantes y los caminos de rodadura, los rodamientos de rodillos, por ejemplo, de rodillos cilíndricos (fig 19a) o de rodillos cónicos (fig 19b), son más rígidos que los rodamientos de bolas.

Fig. 19a

Fig. 19b
3.2.1.7.- Desplazamiento axial
Los rodamientos libres deberán permitir el desplazamiento axial del eje, de manera que los rodamientos no se sobrecarguen, por ejemplo, a causa de la dilatación térmica del eje. Entre los rodamientos más adecuados para una disposición libre, se encuentran los rodamientos de agujas y los rodamientos de rodillos cilíndricos tipo NU y N (fig 20). También se pueden usar rodamientos de rodillos cilíndricos tipo NJ y algunos rodamientos llenos de rodillos cilíndricos.
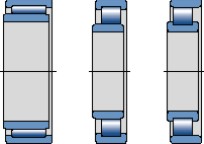
Fig. 20
3.2.1.8.- Montaje y desmontaje
Montaje y Desmontaje de Rodamientos (Recuperado de https://youtu.be/B1sv7JBWpcc)
Los rodamientos con agujero cilíndrico son más fáciles de montar y desmontar si son de diseño desmontable, especialmente si se necesitan ajustes de apriete en ambos aros. Los rodamientos desmontables, también son preferibles cuando el rodamiento ha de ser montado y desmontado con frecuencia, ya que el aro con los elementos rodantes y la jaula, se pueden montar de forma independiente del otro aro, como es el caso de los rodamientos rígidos de bolas con cuatro puntos de contacto y los rodamientos de rodillos cilíndricos, de agujas y cónicos (fig 21) así como los rodamientos axiales de bolas y de rodillos cilíndricos.
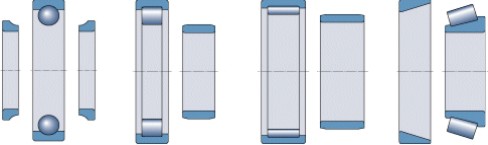
Fig. 21
Los rodamientos con agujero cónico (fig 22) se pueden montar fácilmente sobre un eje cónico o sobre un eje cilíndrico usando un manguito de fijacion o de desmontaje (fig 23) o un manguito escalonado.
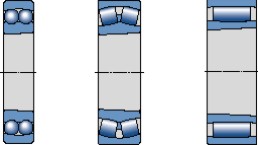
Fig. 22

Fig. 23
3.2.1.9.- Obturaciones integradas
Placas de protección (fig. 24)
Obturaciones de baja fricción (fig. 25)
Obturaciones rozantes (fig. 29)
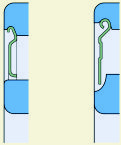
Fig. 24

Fig. 25
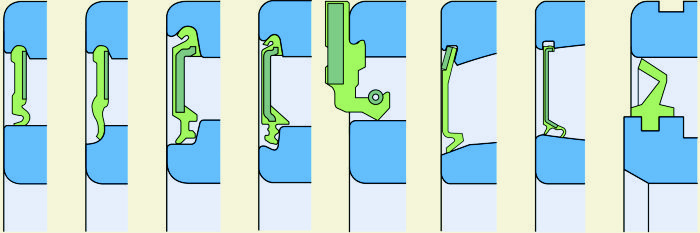
Fig. 26
Que pueden proporcionar una solución económica y compacta para muchas aplicaciones. Se dispone de una gran variedad de tamaños para:
Rodamientos rígidos de bolas
Rodamientos de bolas con contacto angular
Rodamientos de bolas a rótula
Rodamientos de rodillos cilíndricos
Rodamientos de agujas
Rodamientos de rodillos a rótula
Rodamientos CARB
Rodillos de leva
Rodamientos Y, y unidades de rodamientos Y.
Todos los rodamientos con obturaciones integradas a ambos lados están lubricados con una grasa de alta calidad, y en la cantidad adecuada.
Guía de selección de tipo de rodamiento.
Grafico 3.2.1
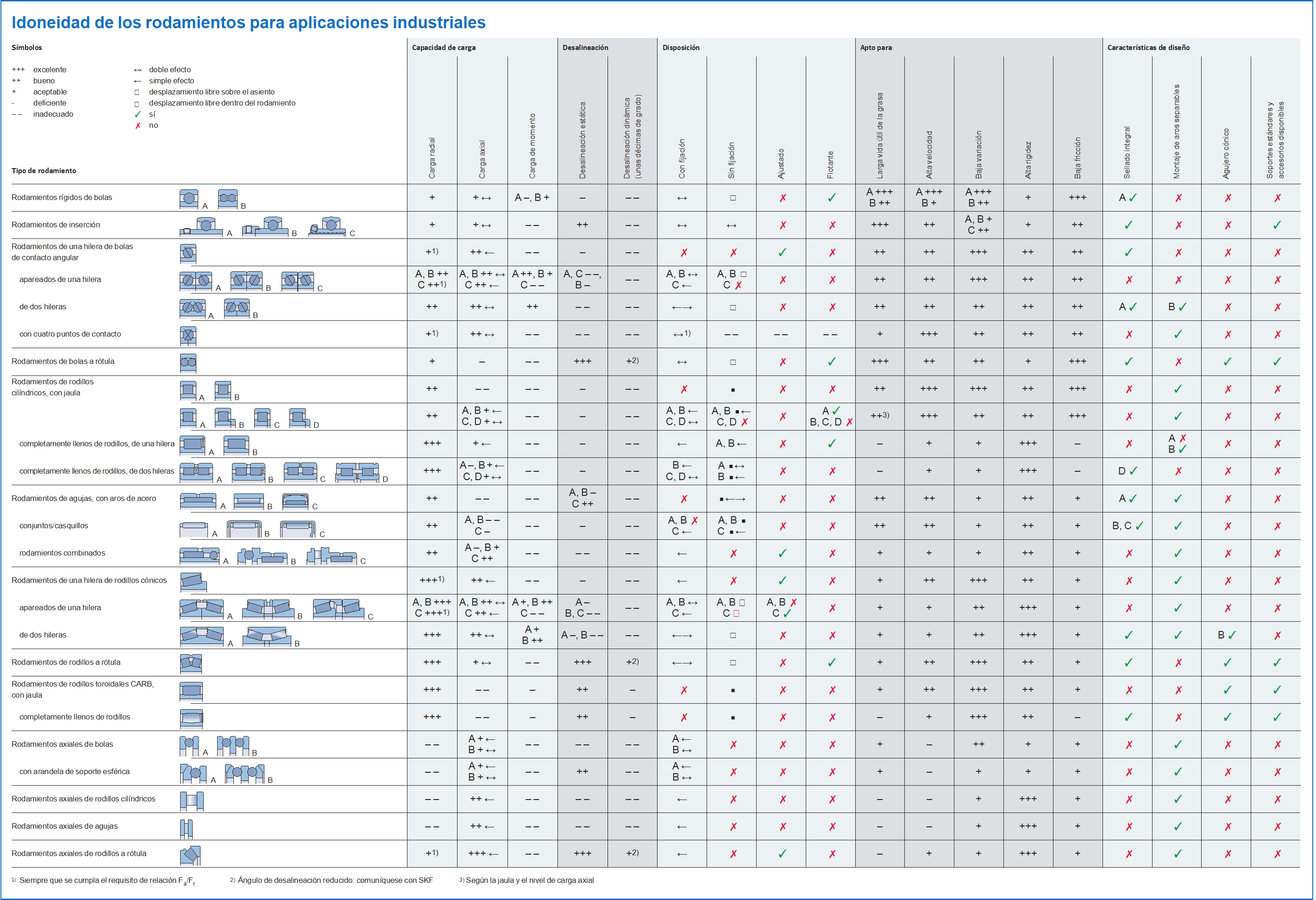
Fuente: Catálogo General SKF
La selección de la obturación es de vital importancia para el adecuado funcionamiento del rodamiento.
3.2.2.- Selección del tamaño del rodamiento.
Se dice y entiéndase, que el rodamiento esta solicitado dinámicamente cuando éste esta girando a una determinada velocidad y está sometido a cargas radiales, axiales o combinadas producidas por acción directa, momentos, deflexiones, etc.
Cuando el elemento rodante de un cojinete antifricción entra en la zona de carga, se originan esfuerzos hertzianos en el aro interno, el propio elemento rodante y aro externo. Debido a que la curvatura de los elementos de contacto es diferente en la dirección axial respecto de la dirección radial, Si un cojinete se mantiene limpio y bien lubricado, se monta y se sella contra la entrada de suciedad o polvo, se conserva en esta condición y es operado a temperaturas razonables, entonces la fatiga del metal será la única causa de falla. En condiciones ideales la falla por fatiga consistirá en una astilladura o descascarado de las superficies que soportan la carga. La norma de la AntiFrictionBearingManufacturersAssociation (AFBMA) indica que el criterio de falla es la primera evidencia de aparición de la fatiga.
Capacidad de carga: Estática y Dinámica.
Las cargas estáticas que tienen componentes radiales y axiales se deben convertir a una carga estática equivalente. Ésta se define como la carga hipotética (radial para los rodamientos radiales y axial para los rodamientos axiales) que, de ser aplicada, causaría en el rodamiento la misma carga máxima sobre los elementos rodantes que las cargas reales. Se obtiene con la siguiente ecuación general:
![]()
Donde:
C0 : Carga estática equivalente
X0 : Factor de carga radial del rodamiento.
Fr : Carga radial real del rodamiento
Y0 : Factor de carga axial del rodamiento
Fa : Carga axial real del rodamiento
La Capacidad de Carga Estática: Se aplica a los cálculos cuando los rodamientos giran a velocidades menores de 10 r/min, están sujetos a movimientos oscilantes muy lentos o permanecen estacionarios bajo carga durante determinados períodos de tiempo.
Las cargas estáticas no son solo las que se aplican cuando el rodamiento está parado o con velocidades de giro muy bajas; deben tenerse en cuenta las cargas de choque pesadas (cargas de duración muy breve). Unas cargas estáticas excesivas pueden comprometer la integridad de un rodamiento provocando deformaciones plásticas en las superficies de contacto.
La capacidad de Carga Dinámica: Se usa para los cálculos de vida de rodamientos sometidos a esfuerzos dinámicos, como los que giran bajo carga. Esta capacidad, definida en la norma ISO 281, expresa la carga del rodamiento que ofrecerá una vida nominal (L10) de un millón de revoluciones. Las cargas dinámicas se deben comprobar utilizando un ciclo de trabajo representativo o espectro de las condiciones de carga del rodamiento, incluyendo las posibles cargas de pico (pesadas) que puedan ocurrir. La capacidad de carga dinámica C se usa para los cálculos en que intervienen rodamientos sometidos a esfuerzo dinámicos, es decir, al seleccionar un rodamiento que gira sometido a carga, y expresa la carga que puede soportar el rodamiento alcanzando una vida nominal de 1.000.000 de revoluciones.
Ecuación de la duración dinámicamente L10.
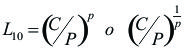
Donde:
L10 : Duración elemental [106rev]
C : Capacidad de carga dinámica elemental (los valores Cr, Ca se indican en la parte de tablas) [kN]
P : Carga dinámica equivalente del rodamiento (las fórmulas para el cálculo Pr, Pa aparecen aquí y en cada serie de construcción de los rodamientos) [kN]
p : exponente:
p = 3, para rodamientos de bolas
p = 10/3, para rodamientos de rodillos cilíndricos, de agujas, cónicos y rodamientos de rodillos a rótula.
El tamaño del rodamiento para una aplicación se selecciona inicialmente en base a su capacidad de carga, en relación con las cargas que tendrá que soportar, y según las exigencias de duración y fiabilidad. En las tablas de productos se indican los valores para la capacidad de carga dinámica C y la capacidad de carga estática C0.
Las condiciones de carga estática y dinámica del rodamiento se deben verificar independientemente. Se deben verificar las cargas dinámicas utilizando un espectro representativo de las condiciones de carga del rodamiento. Dicho espectro debe incluir todas las cargas de pico (elevadas) que se puedan producir en ocasiones excepcionales. Las cargas estáticas no sólo son aquéllas aplicadas al rodamiento en reposo o a bajas velocidades (n < 10 rpm), sino que también deben incluir la verificación de la seguridad estática de las cargas de choque muy elevadas (cargas de duración muy breve).
La dimensión necesaria de los rodamientos se define en función de las fuerzas exteriores actuantes y de acuerdo con la durabilidad y seguridad del rodamiento en el alojamiento. Para la elección del tipo y tamaño del rodamiento son decisivos el tamaño, la dirección y el carácter de la carga que actúa sobre el rodamiento así como la velocidad de giro. Además hay que respetar otras condiciones particulares o especiales de cada alojamiento, como ejemplo la temperatura de funcionamiento, la limitación del espacio, la simplicidad del montaje, los requisitos de lubricación, la empaquetadura etc., que pueden influir sobre la selección del rodamiento más conveniente. En muchos casos, a unas condiciones dadas de funcionamiento, pueden corresponder varios tipos de rodamientos.
3.2.2.1.- Teoría sobre la vida y fiabilidad de los rodamientos.
En la fórmula de la vida SKF, se tiene en cuenta la tensión provocada por las cargas externas, junto con las tensiones originadas por la topografía de la superficie, la lubricación y la cinemática de las superficies de contacto. La influencia de esta combinación de tensiones sobre la vida del rodamiento permite predecir mejor el funcionamiento real del rodamiento en una aplicación determinada.
Debido a su complejidad, no se incluye una descripción detallada de esta teoría. Por tanto, aquí sólo se presenta un planteamiento simplificado bajo el encabezado “Vida nominal SKF”. Esto le permite al usuario explotar al máximo el potencial de vida del rodamiento, realizar reducciones de tamaño controladas y reconocer la influencia de la lubricación y la contaminación en la vida del rodamiento.
Por regla general, el principal fallo en los rodamientos es a causa de la fatiga del metal de las superficies de contacto. Por tanto, para seleccionar el tamaño de un rodamiento para una aplicación determinada, generalmente basta con un criterio basado en la fatiga del camino de rodadura. Las normativas internacionales, como por ejemplo la ISO 281, se basan en la fatiga del metal de las superficies de contacto. Sin embargo, es importante recordar que el rodamiento completo se puede considerar como un sistema en el que la vida de cada componente, es decir, la jaula, el lubricante y la obturación (fig. 27), si la hubiese, contribuye por igual a la resistencia del rodamiento, en algunos casos de manera dominante. En teoría, la vida útil óptima se obtiene cuando todos los componentes logran la misma duración.
En otras palabras, la vida calculada corresponderá a la vida útil real del rodamiento cuando la vida de los otros componentes sea como mínimo de la misma duración que la vida del rodamiento. Entre los otros componentes se pueden incluir la jaula, la obturación y el lubricante. En la práctica, el factor dominante suele ser la fatiga del metal.
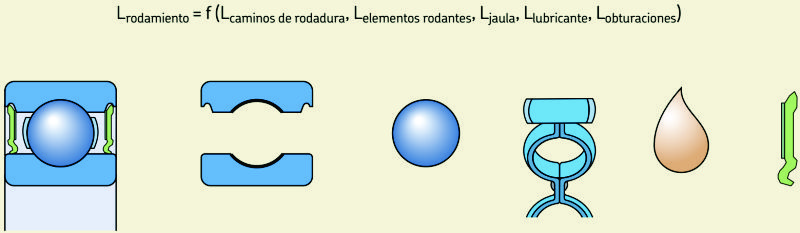
Fig. 27
3.2.2.2.- Capacidad de carga y vida.
a).- Capacidad dinámicas y vida.
La capacidad de carga dinámica C se usa en los cálculos para los rodamientos sometidos a esfuerzos dinámicos, es decir, rodamientos que giran bajo carga. Expresa la carga que dará una vida nominal, según la normativa ISO 281:1990, de 1 000 000 revoluciones. Se asume que la magnitud y el sentido de la carga son constantes, y que es radial para los rodamientos radiales y axial y centrada para los rodamientos axiales.
La vida de un rodamiento se define como:
el número de revoluciones o
el número de horas de funcionamiento a una velocidad determinada
que el rodamiento puede soportar antes de que se manifieste el primer síntoma de fatiga del metal (desconchado, descascarillado) en uno de sus aros o elementos rodantes.
b).- Capacidad estáticas.
La capacidad de carga estática CO se usa en los cálculos cuando los rodamientos:
giran a velocidades muy bajas (n < 10 rpm)
realizan movimientos oscilantes muy lentos
permanecen estacionarios bajo carga durante largos períodos de tiempo.
Convencionalmente se define (según ISO 76-1987),como la carga que provoca entre el contacto anillo-cuerpo rodante, una deformación total permanente de 10-4 veces el ø del cuerpo rodante. Su valor es:
- 4600 MPa para rodamientos de bolas a rótula.
- 4200 MPa para todos los demás rodamientos de bolas.
- 4000 MPa para rodamientos de rodillos.
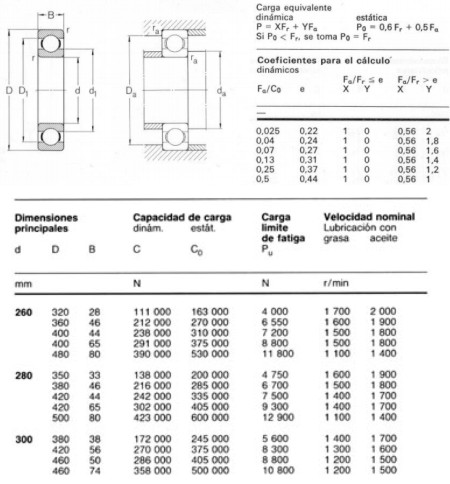
Ante la necesidad de trabajar con estos elementos, es recomendable que se adquiera un catalogo de rodamientos de la marca que prefiera para conocer la numeración y dimensiones del rodamiento que desea indicar. En ese catalogo aparecen además valores de resistencia mecánica que son la base para los cálculos de vida útil. Estos valores ha sido obtenidos en bancos de prueba realizando numerosos ensayos y son los siguientes:
Capacidad de carga estática: C0 (fuerza) Capacidad de carga dinámica: C (fuerza) Velocidad nominal: V (r.p.m.) Carga límite de fatiga: Pu (fuerza)
|
Tabla 3.2.1 |
|
Fig. 3.2.1 |
La falla principal de los rodamientos es la fatiga superficial en las pistas de rodadura y en los elementos rodantes. Esta falla se basa en las fórmulas de esfuerzo de contacto (Hertz). Se han desarrollado cálculos avanzados para estimar la magnitud de estas fuerzas y por otra parte se han desarrollado materiales que soporten estas cargas logrando prolongar la vida útil. En la figura, se aprecia la falla por fatiga superficial en la pista de rodadura del aro interior de un rodamiento radial, esta falla provoca la aparición de escamas que se separan dañando la zona de rodadura. La razón para este tipo de falla se explica evaluando las fórmulas de esfuerzo de contacto, que entregan valores altos bajo la superficie de rodadura provocando la aparición y propagación de fisuras que terminan por cortar la capa superficial de la pista. |
Una composición de rodamientos no solo se compone de una determinado numero de rodamientos, sino que también incluye los componentes asociados con ellos (ejes, soportes, etc). El lubricante es también muy importante y, en la mayoría de los casos, se precisa proteger los rodamientos mediante obturaciones para evitar la perdida de lubricante y la entrada de humedad y otros contaminantes.
El diseño de una de una disposición de rodamientos exige la selección de un tipo adecuado de rodamiento y la disposición adecuada del tamaño de rodamiento, pero eso no basta, también hay que considerar otros aspectos: tipo y la cantidad de lubricante, ajuste y juego interno del rodamiento apropiados, forma adecuada de los demás componentes de la disposición, obturaciones eficaces, etc. cada decisión individual influye en el rendimiento, la fiabilidad y la economía de la disposición de los rodamientos.
|
Disposición de rodamientos |
|
3.2.2.3.- Selección del tamaño del rodamiento utilizando las fórmulas de la vida.
a).- Vida Nominal.
La vida nominal de un rodamiento según la normativa ISO 281:1990 es:
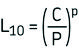
Si la velocidad es constante, suele ser preferible calcular la vida expresada en horas de funcionamiento utilizando la ecuación:
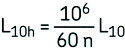
Donde:
L10 = vida nominal (con un 90 % de fiabilidad), millones de revoluciones
L10h= vida nominal (con un 90 % de fiabilidad), horas de funcionamiento
C = capacidad de carga dinámica, kN
P = carga dinámica equivalente del rodamiento, kN
n = velocidad de giro, rpm
p = exponente de la ecuación de la vida
= 3 para los rodamientos de bolas
= 10/3 para los rodamientos de rodillos
b).- Vida Nominal SKF.
Para los rodamientos modernos de alta calidad, la vida nominal o básica se puede desviar significativamente de la vida de servicio real en una aplicación determinada. La vida de servicio en una aplicación depende de una variedad de factores, entre los que se encuentra la lubricación, el grado de contaminación, la desalineación, el montaje adecuado y las condiciones ambientales.
Por este motivo, la normativa ISO 281:1990/Amd 2:2000 contiene una fórmula de la vida ajustada para complementar la vida nominal. Este cálculo de la vida usa un factor de ajuste para tener en cuenta las condiciones de lubricación y contaminación del rodamiento y el límite de fatiga del material.
La normativa ISO 281:1990/Amd 2:2000 también permite que los fabricantes de rodamientos recomienden un método adecuado para calcular el factor de ajuste de la vida a aplicar a un rodamiento en base a las condiciones de funcionamiento. El factor de ajuste de la vida aSKF aplica el concepto de carga límite de fatiga Pu análogo al utilizado cuando se realizan cálculos para otros componentes de la máquina. Los valores para la carga límite de fatiga se encuentran en las tablas de productos. Asimismo, con el fin de reflejar las condiciones de funcionamiento de la aplicación, el factor de ajuste de la vida aSKF hace uso de las condiciones de lubricación (relación de viscosidad k) y del factor ![]() para el nivel de contaminación.
para el nivel de contaminación.
La ecuación para la vida nominal SKF cumple con la normativa ISO 281:1990/Amd 2:2000
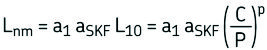
Si la velocidad es constante, la vida puede expresarse en horas de funcionamiento usando la ecuación
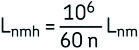
Donde:
Lnm = vida nominal SKF (con un 100 – n% de fiabilidad), millones de revoluciones
- El factor n% representa la probabilidad de fallo, es decir, la diferencia entre la fiabilidad requerida y el 100 %
Lnmh = vida nominal SKF (con un 100 – n% de fiabilidad), horas de funcionamiento
L10 = vida nominal básica (con un 90 % de fiabilidad), millones de revoluciones
a1 = factor de ajuste de la vida para una mayor fiabilidad (Tabla 1)
aSKF = factor de ajuste de la vida SKF (Diagramas 1 al 4)
C = capacidad de carga dinámica, kN
P = carga dinámica equivalente del rodamiento, kN
n = velocidad de giro, rpm
p = exponente de la ecuación de la vida
En algunas ocasiones resulta preferible expresar la vida del rodamiento en unidades distintas a millones de revoluciones u horas. Por ejemplo, la vida de los rodamientos de mangueta usados en automóviles y ferrocarriles se suele expresar en kilómetros recorridos. La tabla 2, ofrece los factores de conversión normalmente utilizados para facilitar el cálculo de la vida del rodamiento en diferentes unidades.
c).- Factor de ajuste de la vida aSKF de SKF
Como ya hemos mencionado, este factor representa la relación existente entre el coeficiente de la carga límite de fatiga (Pu/P), las condiciones de lubricación (relación de viscosidad k) y el nivel de contaminación del rodamiento (![]() ). Los valores para el factor aSKF se pueden obtener de cuatro diagramas, dependiendo del tipo de rodamiento, como función de
). Los valores para el factor aSKF se pueden obtener de cuatro diagramas, dependiendo del tipo de rodamiento, como función de ![]() (Pu/P) para los rodamientos SKF estándar y SKF Explorer y los diferentes valores de la relación de viscosidad k (Diagramas del 1 al 4):
(Pu/P) para los rodamientos SKF estándar y SKF Explorer y los diferentes valores de la relación de viscosidad k (Diagramas del 1 al 4):
Estos diagramas se basan en los valores típicos y en el tipo de factores de seguridad normalmente asociados con las cargas límites de fatiga para otros componentes mecánicos. Teniendo en cuenta las simplificaciones inherentes de la ecuación de la vida nominal SKF, incluso con unas condiciones de funcionamiento identificadas con exactitud, no tiene sentido usar valores para askf superiores a 50.
Diagrama 1: Rodamientos radiales de bolas.
Ver Diagrama 1: Factor aSKF para Rodamientos radiales de bolas.
Diagrama 2: Rodamientos radiales de rodillos.
Ver Diagrama 2: Factor aSKF para Rodamientos radiales de rodillos.
Diagrama 3: Rodamientos axiales de bolas.
Ver Diagrama 3: Factor aSKF para Rodamientos axiales de bolas.
Diagrama 4: Rodamientos axiales de rodillos.
Ver Diagrama 4: Factor aSKF para Rodamientos axiales de rodillos.
Cálculo del factor de ajuste de la vida aSKF
Los programas de ingeniería SKF – SKF Bearing Select, o el “Catáologo Interactivo de Ingeniería SKF”, disponible a través de la página web www.skf.com – también se pueden utilizar para facilitar el cálculo de aSKF. Asimismo, SKF ha desarrollado sofisticados programas informáticos que incorporan la tensión de las superficies de contacto a la ecuación de la vida nominal SKF, permitiendo de este modo que se puedan tener en cuenta otros factores influyentes sobre la vida del rodamiento, tales como la desalineación, la flexión del eje y la deformación del alojamiento (sección “Herramientas de cálculo SKF”).
d).- Condiciones de lubricación – relación de viscosidad k
La eficacia del lubricante viene determinada fundamentalmente por el grado de separación entre las superficies de contacto de rodadura. Para que se forme una película de lubricante adecuada, éste debe tener una viscosidad mínima cuando la aplicación alcance su temperatura de funcionamiento normal. Las condiciones del lubricante se describen según la relación de viscosidad k como la relación entre la viscosidad real del lubricante n y la viscosidad n1 necesaria para una lubricación adecuada, teniendo en cuenta ambos valores cuando el lubricante está a una temperatura de funcionamiento normal,
![]()
donde:
![]() = relación de viscosidad
= relación de viscosidad
![]() = viscosidad real de funcionamiento del lubricante, mm2/s
= viscosidad real de funcionamiento del lubricante, mm2/s
![]() = viscosidad nominal dependiendo del diámetro medio del rodamiento y de la velocidad de giro, mm2/s
= viscosidad nominal dependiendo del diámetro medio del rodamiento y de la velocidad de giro, mm2/s
El lubricante debe mantener una viscosidad mínima a la temperatura de funcionamiento para que se pueda formar una película de lubricante adecuada entre las superficies de rodadura. La viscosidad nominal ![]() , requerida para una lubricación adecuada se puede calcular con el diagrama 5, usando el diámetro medio del rodamiento dm = 0.5 (d + D), mm, y la velocidad de giro del rodamiento n, rpm. Este diagrama ha sido revisado teniendo en cuenta los últimos hallazgos en tribología de rodamientos.
, requerida para una lubricación adecuada se puede calcular con el diagrama 5, usando el diámetro medio del rodamiento dm = 0.5 (d + D), mm, y la velocidad de giro del rodamiento n, rpm. Este diagrama ha sido revisado teniendo en cuenta los últimos hallazgos en tribología de rodamientos.
Si, por experiencia, se conoce la temperatura de funcionamiento, o si se puede determinar de otra manera, la viscosidad correspondiente a la temperatura de referencia normalizada internacionalmente de 40 °C se puede obtener del diagrama 6. El diagrama corresponde a un índice de viscosidad de 95. La tabla 3 indica los grados de viscosidad según la normativa ISO 3448:1992, mostrando la gama de viscosidad para cada una de las clases a 40 °C. Determinados tipos de rodamientos, por ejemplo los rodamientos de rodillos a rótula, los rodamientos de rodillos cónicos y los rodamientos axiales de rodillos a rótula tienen normalmente una temperatura de funcionamiento superior a la de otros rodamientos, por ejemplo los rodamientos rígidos de bolas y los rodamientos de rodillos cilíndricos, bajo unas condiciones de funcionamiento similares.
Ejemplo de cálculo
Un rodamiento con un diámetro de agujero d = 340 mm y un diámetro exterior D = 420 mm debe funcionar a una velocidad de n = 500 rpm. Puesto que dm = 0,5 (d + D), dm = 380 mm, según el diagrama 5, la viscosidad mínima ![]() requerida para lograr una lubricación apropiada a la temperatura de funcionamiento es de aproximadamente 11 mm2/s. En el diagrama 6, suponiendo que la temperatura de funcionamiento del rodamiento es de 70 °C, vemos que se requerirá un lubricante según la clase de viscosidad ISO VG 32, con una viscosidad real
requerida para lograr una lubricación apropiada a la temperatura de funcionamiento es de aproximadamente 11 mm2/s. En el diagrama 6, suponiendo que la temperatura de funcionamiento del rodamiento es de 70 °C, vemos que se requerirá un lubricante según la clase de viscosidad ISO VG 32, con una viscosidad real ![]() de al menos 32 mm2/s a la temperatura de referencia de 40 °C.
de al menos 32 mm2/s a la temperatura de referencia de 40 °C.
e).- Consideración de los aditivos EP
Se sabe que la presencia de algunos aditivos EP en el lubricante puede prolongar la vida útil del rodamiento cuando, de lo contrario, la lubricación sería insuficiente, por ejemplo, si k < 1 y el factor para el nivel de contaminación ![]() = 0.2, según la normativa DIN ISO 281 Addendum 1:2003, se podría usar en el cálculo un valor k = 1 si se usa un lubricante con aditivos EP de probada eficacia. En este caso, el factor de ajuste de la vida aSKF debe estar limitado a =< 3, pero no debe ser inferior al factor aSKF para los lubricantes normales.
= 0.2, según la normativa DIN ISO 281 Addendum 1:2003, se podría usar en el cálculo un valor k = 1 si se usa un lubricante con aditivos EP de probada eficacia. En este caso, el factor de ajuste de la vida aSKF debe estar limitado a =< 3, pero no debe ser inferior al factor aSKF para los lubricantes normales.
Para el resto de la gama, se puede determinar el factor de ajuste de la vida aSKF usando la relación de viscosidad k real de la aplicación. Si la contaminación es abundante, es decir, el factor de contaminación ![]() < 0,2, se deberán comprobar los posibles beneficios del aditivo EP mediante la realización de pruebas. Se deberá consultar la información relacionada con los aditivos EP.
< 0,2, se deberán comprobar los posibles beneficios del aditivo EP mediante la realización de pruebas. Se deberá consultar la información relacionada con los aditivos EP.
f).- Factor ![]() para el nivel de contaminación
para el nivel de contaminación
Este factor ha sido introducido con el fin de tener en cuenta el nivel de contaminación del lubricante a la hora de calcular la vida del rodamiento. La influencia de la contaminación en la fatiga del rodamiento depende de una serie de parámetros entre los que se incluyen el tamaño del rodamiento, el espesor relativo de la película de lubricante, el tamaño y la distribución de las partículas contaminantes sólidas, los tipos de contaminante (blando, duro), etc. La influencia de estos parámetros en la vida del rodamiento es compleja y muchos de ellos son difíciles de cuantificar. Por tanto, no es fácil asignar a ![]() valores precisos que puedan tener validez general. No obstante, en la tabla 4 se ofrecen algunos valores orientativos
valores precisos que puedan tener validez general. No obstante, en la tabla 4 se ofrecen algunos valores orientativos
Si el rodamiento se usa en una aplicación de forma satisfactoria y los cálculos de la vida anterior se basaron en el uso del factor de ajuste antiguo a23, entonces se puede obtener un factor correspondiente (valor implícito) ![]() para obtener un valor aSKF equivalente al ajuste a23 como se explica en la sección “Un caso especial – el factor de ajuste a23”
para obtener un valor aSKF equivalente al ajuste a23 como se explica en la sección “Un caso especial – el factor de ajuste a23”
Se debe advertir que este sistema probablemente indique sólo un valor aproximado del factor ![]() efectivo para el nivel de contaminación de la aplicación. Un segundo método para obtener un valor para el factor
efectivo para el nivel de contaminación de la aplicación. Un segundo método para obtener un valor para el factor ![]() que sea representativo para una aplicación consiste en la cuantificación del nivel de contaminación del lubricante como dato para la evaluación del valor para el factor
que sea representativo para una aplicación consiste en la cuantificación del nivel de contaminación del lubricante como dato para la evaluación del valor para el factor ![]() .
.
g).- Clasificación ISO de la contaminación y valuación del filtro
El método estándar para clasificar el nivel de contaminación en un sistema de lubricación se describe en la normativa ISO 4406:1999. En este sistema de clasificación, el resultado del recuento de las partículas sólidas se convierte en un código con una escala numérica, (tabla 5 y diagrama 7).
Uno de los métodos para comprobar el nivel de contaminación del aceite del rodamiento es el método de recuento con microscopio. Con este
método de recuento se utilizan dos numeraciones, relacionadas con el número de partículas >= 5 ![]() m y >= 15
m y >= 15 ![]() m. Otro método hace referencia a los contadores automáticos de partículas, en los que se usan tres numeraciones relacionadas con el número de partículas = 4
m. Otro método hace referencia a los contadores automáticos de partículas, en los que se usan tres numeraciones relacionadas con el número de partículas = 4 ![]() m, >= 6
m, >= 6 ![]() m y >= 14
m y >= 14 ![]() m. La clasificación del nivel de contaminación incluye tres numeraciones.
m. La clasificación del nivel de contaminación incluye tres numeraciones.
Algunos ejemplos típicos de las clasificaciones del nivel de contaminación para el aceite lubricante son /15/12 (A) ó 22/18/13 (B), tal y como se muestra en el diagrama 7.
El ejemplo A significa que el aceite contiene entre 160 y 230 partículas >= 5 ![]() m y entre 20 y 40 partículas >= 15
m y entre 20 y 40 partículas >= 15 ![]() m por mililitro de aceite.
Aunque lo ideal sería que los aceites lubricantes fuesen continuamente filtrados, la viabilidad de un sistema de filtrado dependerá de la optimización entre el aumento de los costes y el incremento del rendimiento del rodamiento.
m por mililitro de aceite.
Aunque lo ideal sería que los aceites lubricantes fuesen continuamente filtrados, la viabilidad de un sistema de filtrado dependerá de la optimización entre el aumento de los costes y el incremento del rendimiento del rodamiento.
Una valuación del filtro indica la eficacia del mismo. La eficacia del filtro se define como la valuación del filtro o factor de reducción ![]() , que está relacionado con un tamaño determinado de partícula. Cuanto mayor sea el valor de
, que está relacionado con un tamaño determinado de partícula. Cuanto mayor sea el valor de ![]() , más eficaz será el filtro para el tamaño de partícula especificado. Por tanto, se deben considerar tanto el valor de
, más eficaz será el filtro para el tamaño de partícula especificado. Por tanto, se deben considerar tanto el valor de ![]() como el tamaño específico de la partícula. La valuación del filtro
como el tamaño específico de la partícula. La valuación del filtro ![]() es expresada como la relación entre el número de partículas especificadas antes y después del filtrado. Se puede calcular del siguiente modo:
es expresada como la relación entre el número de partículas especificadas antes y después del filtrado. Se puede calcular del siguiente modo:
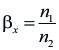
Donde:
![]() = valuación del filtro relacionada con un tamaño de partícula especificado x
= valuación del filtro relacionada con un tamaño de partícula especificado x
x = tamaño de las partículas, ![]() m
m
n1 = número de partículas por unidad de volumen (100 ml) mayores que x ![]() m sin pasar por el filtro
m sin pasar por el filtro
n2 = número de partículas por unidad de volumen (100 ml) mayores que x ![]() m filtradas
m filtradas
h).- Determinación de ![]() cuando se conoce el nivel de contaminación
cuando se conoce el nivel de contaminación
En la lubricación con aceite, una vez que se conoce el nivel de contaminación del mismo, bien mediante el recuento con microscopio o mediante el análisis del recuento automático de partículas descrito en la normativa ISO 4406:1999, o indirectamente como resultado de la relación de filtración aplicada al sistema de circulación de aceite, esta información se puede usar para determinar el factor ![]() para el nivel de contaminación. Se debe tener en cuenta que el factor hc no se puede obtener exclusivamente de la contaminación del aceite. Depende en gran medida de las condiciones de lubricación, es decir, de k y del tamaño del rodamiento. En estas páginas se presenta un método simplificado para obtener el factor
para el nivel de contaminación. Se debe tener en cuenta que el factor hc no se puede obtener exclusivamente de la contaminación del aceite. Depende en gran medida de las condiciones de lubricación, es decir, de k y del tamaño del rodamiento. En estas páginas se presenta un método simplificado para obtener el factor ![]() para una aplicación determinada según la normativa DIN ISO 281 Addendum 4:2003. El factor hc se obtiene del código de contaminación del aceite (o relación de filtrado de la aplicación), utilizando el diámetro medio del rodamiento dm = 0,5 (d + D), en mm, y la relación de viscosidad k del mismo (diagrama 8 y 9).
para una aplicación determinada según la normativa DIN ISO 281 Addendum 4:2003. El factor hc se obtiene del código de contaminación del aceite (o relación de filtrado de la aplicación), utilizando el diámetro medio del rodamiento dm = 0,5 (d + D), en mm, y la relación de viscosidad k del mismo (diagrama 8 y 9).
Los diagrama 8 y 9 ofrecen los valores típicos del factor ![]() para la lubricación por circulación de aceite con diferentes grados de filtrado de aceite y códigos de contaminacióndel mismo. En las aplicaciones en las que el baño de aceite no muestra prácticamente ningún aumento en las partículas de contaminación presentes en el sistema, se pueden aplicar factores de contaminación similares. Por otra parte, si el número de partículas en el baño de aceite continúa aumentando con el paso del tiempo, debido a un desgaste excesivo o a la introducción de contaminantes, se debe reflejar en la selección del factor
para la lubricación por circulación de aceite con diferentes grados de filtrado de aceite y códigos de contaminacióndel mismo. En las aplicaciones en las que el baño de aceite no muestra prácticamente ningún aumento en las partículas de contaminación presentes en el sistema, se pueden aplicar factores de contaminación similares. Por otra parte, si el número de partículas en el baño de aceite continúa aumentando con el paso del tiempo, debido a un desgaste excesivo o a la introducción de contaminantes, se debe reflejar en la selección del factor ![]() usado para el baño de aceite como se indica en la normativa DIN ISO 281 Addendum 4:2003.
usado para el baño de aceite como se indica en la normativa DIN ISO 281 Addendum 4:2003.
También se puede determinar ![]() para la lubricación con grasa de un modo similar, aunque la contaminación puede ser difícil de cuantificar y por ello se define de un modo simple y cualitativo.
para la lubricación con grasa de un modo similar, aunque la contaminación puede ser difícil de cuantificar y por ello se define de un modo simple y cualitativo.
Los diagrama 10 y 11, ofrecen los valores típicos del factor hc para la lubricación con grasa en condiciones de funcionamiento de limpieza extrema y normal.
Para otros grados de contaminación relacionados con la lubricación por circulación de aceite, con baño de aceite y con grasa, consulte la normativa DIN ISO 281 Addendum 4:2003 o al departamento de Ingeniería de Aplicaciones de SKF.
El siguiente ejemplo muestra el gran efecto de la contaminación sobre la vida a fatiga. En un entorno altamente contaminado (una caja
de engranajes con un número considerable de partículas de desgaste) se probaron varios rodamientos rígidos de bolas 6305 con y sin obturaciones. No se produjo ningún fallo en los rodamientos obturados, y las pruebas se interrumpieron por razones prácticas después de que los rodamientos obturados hubiesen funcionado
durante períodos de tiempo como mínimo 30 veces mayores que las vidas experimentales de los rodamientos sin obturar. Las vidas de los rodamientos no obturados supusieron el 0,1 de la vida calculada L10, que se corresponde con el factor ![]() = 0 como se indica en la Tabla 4.
= 0 como se indica en la Tabla 4.
Los diagramas 1 a 4, indican la importancia de la limpieza en la lubricación por la rápida reducción de los valores para el factor aSKF al disminuir ![]() . El uso de obturaciones integrales es un modo muy eficaz y económico de mantener al mínimo la contaminación en los rodamientos.
. El uso de obturaciones integrales es un modo muy eficaz y económico de mantener al mínimo la contaminación en los rodamientos.
i).- Un caso especial – el factor de ajuste a23
En anteriores catálogos SKF, la vida nominal del rodamiento se ajustaba usando el factor a23 para el material y la lubricación. Este factor lo introdujo SKF en 1975.
En la normativa ISO 281:1990/Amd 2:2000 se hace referencia a este tipo de ajuste de la vida como un caso especial del factor de ajuste de la vida aSKF más general. El ajuste a23 implica un valor específico de la “relación contaminación-carga” [![]() (Pu/P)]23 utilizada en los diagramas para el factor de ajuste de vida SKF aSKF. Ya que el factor a23 solamente depende de la relación de viscosidad k, se superpone una escala a23 en las curvas k de los diagramas 1 a 4, para el factor aSKF en el punto en que
(Pu/P)]23 utilizada en los diagramas para el factor de ajuste de vida SKF aSKF. Ya que el factor a23 solamente depende de la relación de viscosidad k, se superpone una escala a23 en las curvas k de los diagramas 1 a 4, para el factor aSKF en el punto en que ![]() (Pu/P) = [
(Pu/P) = [![]() (Pu/P)]23. El factor
(Pu/P)]23. El factor ![]() para el nivel de contaminación será entonces
para el nivel de contaminación será entonces
![]() = [
= [![]() (Pu/P)]23/(Pu/P)
(Pu/P)]23/(Pu/P)
El punto en que ![]() (Pu/P) = [
(Pu/P) = [![]() (Pu/P)]23 está marcado con una línea de puntos y los valores se muestran en la tabla 6 para los rodamientos SKF estándar y para los rodamientos SKF Explorer. Por ejemplo, para los rodamientos radiales de bolas estándar, el factor
(Pu/P)]23 está marcado con una línea de puntos y los valores se muestran en la tabla 6 para los rodamientos SKF estándar y para los rodamientos SKF Explorer. Por ejemplo, para los rodamientos radiales de bolas estándar, el factor ![]() correspondiente es:
correspondiente es:
![]()
El punto de la “relación contaminacióncarga” [![]() (Pu/P)]23 = 0,05 en el diagrama 1, aSKF = a23 y a23 se puede leer directamente en el eje aSKF usando la escala k de la línea de puntos. Entonces, se puede calcular la vida con la ecuación simplificada.
(Pu/P)]23 = 0,05 en el diagrama 1, aSKF = a23 y a23 se puede leer directamente en el eje aSKF usando la escala k de la línea de puntos. Entonces, se puede calcular la vida con la ecuación simplificada.
Lnm = a1 a23 L10
Donde:
Lnm = vida nominal SKF (con un 100 – n % de fiabilidad), millones de revoluciones
L10 = vida nominal (con un 90 % de fiabilidad), millones de revoluciones
a1 = factor de ajuste de la vida para una mayor fiabilidad (tabla 1)
a23 = factor de ajuste para el material y la lubricación, cuando ![]() (Pu/P) = [
(Pu/P) = [![]() (Pu/P)]23 (diagramas 1 a 4)
(Pu/P)]23 (diagramas 1 a 4)
El uso del factor de ajuste a23 implica en la práctica, una condición de tensión caracterizada por un valor de ![]() (Pu/P) = [
(Pu/P) = [![]() (Pu/P)]23. Si el valor
(Pu/P)]23. Si el valor ![]() (Pu/P) actual del rodamiento es menor o mayor que el valor [
(Pu/P) actual del rodamiento es menor o mayor que el valor [![]() (Pu/P)]23, la estimación de vida del rodamiento será demasiado alta o demasiado baja. En otras palabras, el factor de ajuste a23 no representa bien a las aplicaciones con cargas elevadas y mayor contaminación o con cargas ligeras y mayor limpieza.
(Pu/P)]23, la estimación de vida del rodamiento será demasiado alta o demasiado baja. En otras palabras, el factor de ajuste a23 no representa bien a las aplicaciones con cargas elevadas y mayor contaminación o con cargas ligeras y mayor limpieza.
Para los rodamientos estándar que funcionan con una relación de carga C/P de aproximadamente 5, el nivel de contaminación para a23 requerirá un factor ![]() de alrededor de 0,4 a 0,5. Si la limpieza real de la aplicación es inferior al nivel normal, el uso del ajuste a23 lleva a una sobreestimación de la vida del rodamiento. Por tanto, SKF recomienda usar únicamente el método aSKF para lograr una selección del tamaño del rodamiento más fiable.
de alrededor de 0,4 a 0,5. Si la limpieza real de la aplicación es inferior al nivel normal, el uso del ajuste a23 lleva a una sobreestimación de la vida del rodamiento. Por tanto, SKF recomienda usar únicamente el método aSKF para lograr una selección del tamaño del rodamiento más fiable.
La correspondencia entre a23 y aSKF resulta útil para convertir aplicaciones originalmente diseñadas con el factor de ajuste a23 a un factor de ajuste más general aSKF. Muchas aplicaciones que tienen un registro de funcionamiento satisfactorio, calculado inicialmente usando el factor de ajuste a23, pueden convertirse fácilmente a un factor aSKF equivalente.
En la práctica esto implica adoptar un factor de contaminación ![]() de la aplicación basado en las “relaciones contaminacióncarga” [
de la aplicación basado en las “relaciones contaminacióncarga” [![]() (Pu/P)]23 que se muestran en la tabla 6. El factor
(Pu/P)]23 que se muestran en la tabla 6. El factor ![]() conseguido de este modo representa una simple aproximación del factor real
conseguido de este modo representa una simple aproximación del factor real ![]() . Esta primera estimación del factor
. Esta primera estimación del factor ![]() se puede mejorar aún más usando los coeficientes de limpieza del aceite que se describen en la sección “Determinación de hc cuando se conoce el nivel de contaminación”.
se puede mejorar aún más usando los coeficientes de limpieza del aceite que se describen en la sección “Determinación de hc cuando se conoce el nivel de contaminación”.
j).- Cálculo de la vida con condiciones de funcionamiento variables
En las aplicaciones en las que la carga del rodamiento varía a lo largo del tiempo tanto en magnitud como en sentido, con cambios de velocidad, temperatura, condiciones de lubricación y nivel de contaminación, no se puede calcular directamente la vida del rodamiento sin realizar el cálculo intermedio de una carga equivalente relacionada con las condiciones de carga variables. Debido a la complejidad del sistema, este parámetro intermedio no será fácil de determinar y no simplificará la ecuación.
Por tanto, bajo condiciones de funcionamiento fluctuantes, es necesario reducir el espectro de cargas o ciclo de trabajo de la aplicación a un número limitado de casos de cargas más sencillas (diagrama 12). En el caso de una carga continuamente variable, se puede acumular cada nivel de carga diferente y reducir el espectro de cargas a un histograma de bloques de carga constantes, cada uno de ellos caracterizando un determinado porcentaje o fracción de tiempo del funcionamiento de la aplicación. Se debe advertir que las cargas elevadas y medianas consumen la vida del rodamiento a mayor velocidad que las cargas ligeras. Por tanto, resulta importante que las cargas de choque y de pico estén bien representadas en el diagrama de cargas, incluso si son relativamente infrecuentes y están limitadas a pocas revoluciones.
La carga del rodamiento y las condiciones de funcionamiento se pueden promediar a un valor constante dentro de cada intervalo de trabajo o “ciclo”. Asimismo, el número de horas de funcionamiento o revoluciones esperado de cada intervalo de trabajo individual muestra la fracción de vida requerida por esa condición de carga en particular. Así por ejemplo, si denominamos N1 al número de revoluciones necesarias bajo las condiciones de carga P1, y N al ciclo de vida total de la aplicación, entonces la fracción del ciclo de vida U1 = N1/N se utilizará con la condición de carga P1, que tiene una vida calculada de L10m1. Se puede predecir la vida del rodamiento bajo condiciones de carga variables usando la ecuación:
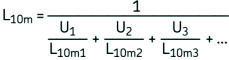
Donde:
L10m = vida nominal SKF (con un 90 % de fiabilidad), millones de revoluciones
L10m1, L10m2, … = vidas nominales SKF (con un 90 % de fiabilidad) bajo las condiciones constantes 1, 2, ..., millones de revoluciones
U1, U2, ... = fracción del ciclo de vida bajo las condiciones 1,2, ... Nota: U1 + U2 + … Un = 1
El uso de este método de cálculo depende en gran medida de la disponibilidad de diagramas de carga representativos para la aplicación. Se debe tener en cuenta que dicho historial de cargas también se puede obtener según las condiciones de funcionamiento típicas o los ciclos de trabajo estándar requeridos por ese tipo de aplicación.
k).- Influencia de la temperatura de funcionamiento
Las dimensiones de un rodamiento en funcionamiento cambian como resultado de las transformaciones estructurales que se producen en el interior del material. La temperatura, el tiempo y la tensión influyen sobre estas transformaciones.
Para evitar cambios dimensionales inadmisibles durante el funcionamiento debido a la transformación estructural, los materiales de los rodamientos se someten a un tratamiento térmico especial (estabilización) (tabla 7).
Los rodamientos estándar hechos de acerosde temple total y de temple por corrientes de inducción tienen una temperatura máxima de funcionamiento recomendada de entre 120 y 200 °C, dependiendo del tipo de rodamiento. Estas temperaturas máximas de funcionamiento están directamente relacionadas con el tratamiento térmico. Puede encontrar información adicional en el texto precedente a la sección de rodamientos.
Si las temperaturas de funcionamiento normales de la aplicación son superiores a la temperatura máxima recomendada, es preferible el uso de un rodamiento con una mayor clase de estabilización.
Para las aplicaciones en las que los rodamientos funcionan a temperaturas elevadas de manera continua, puede que sea necesario ajustar la capacidad de carga dinámica del rodamiento.
El funcionamiento satisfactorio de los rodamientos a temperaturas elevadas, también depende de si el lubricante seleccionado puede o no mantener sus propiedades de lubricación y de la adecuación de los materiales empleados para las obturaciones, jaulas, etc.
Como regla general, deberá contactar con el departamento de Ingeniería de Aplicaciones de SKF si va a utilizar rodamientos que requieran una clase de estabilidad mayor que S1 a altas temperaturas.
l).- Vida nominal requerida
A la hora de determinar el tamaño del rodamiento, es aconsejable verificar la vida nominal SKF calculada con la vida determinada de la aplicación, en caso de conocer ésta última. Normalmente, esto depende del tipo de máquina y de los requisitos relacionados con la duración del servicio y la fiabilidad de funcionamiento. Si no se dispone de experiencia previa, se pueden utilizar los valores orientativos señalados en las tablas 8 y 9
3.2.2.4.- Cargas dinámicas del rodamiento
a).- Cálculo de las cargas dinámicas del rodamiento
Las cargas que actúan sobre un rodamiento se pueden calcular de acuerdo con las leyes de la mecánica siempre que se conozcan o se puedan determinar las fuerzas externas (por ejemplo, fuerzas producidas por la transmisión de potencia, de trabajo, o de inercia). Cuando se calculan las componentes de carga para un rodamiento individual, el eje se considera como una viga que descansa sobre soportes rígidos y no sometidos a momentos, a efecto de simplificar los cálculos. Tampoco se tienen en cuenta las deformaciones elásticas en el rodamiento, el soporte o el bastidor de la máquina, ni los momentos producidos en el rodamiento como resultado de la flexión del eje.
Estas simplificaciones son necesarias cuando se realizan los cálculos de una disposición de rodamientos con la asistencia de medios disponibles como las calculadoras de bolsillo. Los métodos normalizados para el cálculo de las capacidades de carga básica y las cargas equivalentes se basan en suposiciones similares.
Las cargas que actúan sobre un rodamiento se pueden calcular en base a la teoría de la elasticidad sin las suposiciones mencionadas anteriormente, pero esto requeriría el uso de complicados programas informáticos. En estos programas, los rodamientos, el eje y el soporte se consideran como componentes resilientes de un sistema.
Las fuerzas externas de, por ejemplo, los pesos propios de los ejes y de los componentes que éstos soportan, o del peso de un vehículo y otras fuerzas de inercia, o bien se conocen o se pueden calcular. No obstante, cuando se determinan las fuerzas de trabajo (las fuerzas de laminación, las fuerzas de corte en máquina herramienta, etc.), las fuerzas de choque y las fuerzas dinámicas adicionales, por ejemplo, a causa de un desequilibrio, suele ser necesario confiar en estimaciones basadas en la experiencia obtenida con otras máquinas y disposiciones de rodamientos similares.
i).- Trenes de engranajes
En el caso de los trenes de engranajes, las fuerzas teóricas que actúan sobre los dientes se pueden calcular conociendo la potencia transmitida y las características del diseño de los dientes del engranaje. No obstante, hay fuerzas dinámicas adicionales que se producen en el propio engranaje o por el accionamiento o toma de fuerza. Las fuerzas dinámicas adicionales en los engranajes son producto de los errores de forma de los dientes y de los desequilibrios de los elementos que giran. Debido a las exigencias de un funcionamiento silencioso, los engranajes se fabrican según normas muy estrictas de precisión, por ello las fuerzas adicionales son generalmente tan pequeñas que no se deben tener en cuenta en los cálculos para los rodamientos.
Las fuerzas adicionales originadas por el tipo y el modo de funcionamiento de las máquinas con trenes de engranajes sólo se pueden determinar cuando las condiciones de funcionamiento son conocidas. Su influencia sobre la vida nominal de los rodamientos está considerada por un factor de “funcionamiento” que tiene en cuenta las cargas de choque y la eficacia del engranaje. Normalmente, los valores de este factor para las diferentes condiciones de funcionamiento, se pueden encontrar en la información publicada por el fabricante del engranaje.
ii).- Transmisiones por correa
Para calcular las cargas que actúan sobre los rodamientos en el caso de las transmisionespor correa, es necesario tener en cuenta la tracción efectiva de la correa (fuerza periférica), la cual depende del par que se transmita. La tracción de la correa se deberá multiplicar por un factor cuyo valor depende del tipo de correa, de su precarga, de su tensión y de las fuerzas dinámicas adicionales. Los valores de este factor normalmente son publicados por los fabricantes de correas. No obstante, si no hubiese información disponible, se pueden aplicar los siguientes valores para:
correas dentadas = 1,1 a 1,3
correas en V = 1,2 a 2,5
correas planas = 1,5 a 4,5
Los valores más altos se aplican cuando la distancia entre los ejes es corta, para correas bajo cargas elevadas o de choque, o cuando la tensión de la correa es elevada.
b).- Carga dinámica equivalente del rodamiento
Si la carga F del rodamiento obtenida al utilizar la información anterior cumple con los requisitos de la capacidad de carga dinámica C, es decir, si es constante en magnitud y dirección y actúa radialmente sobre un rodamiento radial o axialmente y centrada sobre un rodamiento axial, entonces P = F, pudiendo introducir la carga directamente en las ecuaciones de la vida.
En todos los demás casos, primero es necesario calcular la carga dinámica equivalente del rodamiento. Ésta se define como la carga hipotética, constante en magnitud y dirección, que si actuara radialmente sobre un rodamiento radial o axialmente y centrada sobre un rodamiento axial, tendría el mismo efecto sobre la vida del rodamiento que las cargas reales a las cuales está sometido dicho rodamiento (fig. 2).
Los rodamientos radiales con frecuencia están sometidos a cargas radiales y axiales simultáneamente. Cuando la magnitud y la dirección de la carga resultante son constantes, la carga dinámica equivalente P se puede calcular con la siguiente ecuación general.
P = XFr + YFa
Donde:
P = carga dinámica equivalente del rodamiento, kN
Fr = carga radial real del rodamiento, kN
Fa = carga axial real del rodamiento, kN
X = factor de carga radial del rodamiento
Y = factor de carga axial del rodamiento
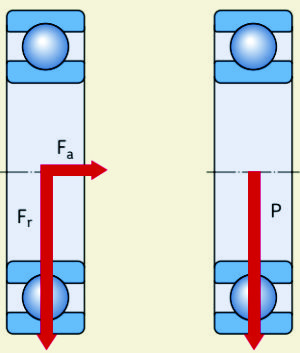
fig. N0 2
|
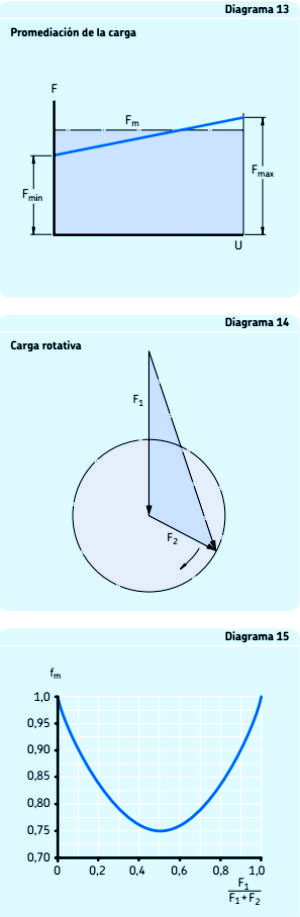
En el caso de los rodamientos radiales de una hilera, una carga axial adicional sólo influye la carga dinámica equivalente P si la relación Fa/Fr excede un determinado factor límite e. Para los rodamientos de dos hileras, incluso las pequeñas cargas axiales influyen de un modo significativo. Esta misma ecuación general también se puede aplicar a los rodamientos axiales de rodillos a rótula, capaces de soportar cargas tanto axiales como radiales. Para los rodamientos axiales que sólo pueden soportar cargas puramente axiales, p.ej. rodamientos axiales de bolas y de rodillos cilíndricos, la ecuación se puede simplificar, siempre que la carga esté centrada, a P = Fa Toda la información y los datos requeridos para calcular la carga dinámica equivalente del rodamiento se encuentra en el texto introductorio de la sección de cada rodamiento y en las tablas de productos. i).- Carga fluctuante del rodamiento En muchos casos la magnitud de la carga fluctúa. Se deberá aplicar la fórmula del cálculo de la vida con condiciones de funcionamiento variables ii).- Carga media dentro de un intervalo de trabajo Dentro de cada intervalo de carga las condiciones de funcionamiento pueden variar ligeramente respecto del valor nominal. Asumiendo que las condiciones de funcionamiento, por ejemplo la velocidad y la dirección de la carga, son bastante constantes y que la magnitud de la carga varía constantemente entre un valor mínimo Fmín y un valor máximo Fmáx (diagrama 13), se puede obtener la carga media a partir de:
iii).- Carga giratoria Si, como se ilustra en el diagrama 14, la carga del rodamiento consta de una carga F1, que es constante en magnitud y sentido (p.ej. el peso de un rotor) y una carga giratoria constante F2 (p.ej. una carga desequilibrada), la carga media se puede obtener usando: Fm = fm(F1 + F2) Encontrará los valores del factor fm en el diagrama 15. |
Diagramas N0 13, 14 y 15
|
c).- Carga mínima requerida
La correlación entre la carga y la vida útil es menos evidente con cargas muy ligeras. En este caso, existen otros factores de fallo distintos a la fatiga
Para que un rodamiento pueda funcionar de un modo satisfactorio, debe estar siempre sometido a una carga mínima. Una regla empírica general indica que los rodamientos de rodillos se deben someter a cargas mínimas correspondientes a 0,02 C, y los de bolas, a cargas mínimas correspondientes a 0,01 C. La importancia de aplicar esta carga mínima a los rodamientos, aumenta cuando éstos están sometidos a grandes aceleraciones o cuando las velocidades superan el 50 % de las velocidades límite indicadas en las tablas de productos (sección “Velocidades y vibración”). Si no se pueden cumplir los requisitos de carga mínima, se debe considerar el uso de rodamientos NoWear.
En el texto que precede las tablas de productos se dan recomendaciones para el cálculo de las cargas mínimas requeridas para cada tipo de rodamiento.
3.2.2.5.- Selección del tamaño del rodamiento utilizando la capacidad de carga estática
El tamaño del rodamiento se deberá seleccionar en base a su capacidad de carga estática C0 y no en base a la vida del rodamiento cuando se produzcan las siguientes condiciones:
El rodamiento es estacionario y está sometido a cargas continuas o intermitentes (de choque).
El rodamiento efectúa lentos movimientos de oscilación o alineación bajo carga.
El rodamiento gira bajo carga a velocidades muy bajas (n < 10 rpm) y sólo se necesita alcanzar una vida corta (en este caso, la ecuación de la vida para una determinada carga equivalente P daría una capacidad de carga dinámica C requerida tan baja, que el rodamiento seleccionado empleando esta fórmula estaría sometido a una sobrecarga durante el servicio).
El rodamiento gira y tiene que soportar elevadas cargas de choque, además de las cargas de funcionamiento normales.
En todos estos casos, la capacidad de carga permisible para el rodamiento no está determinada por la fatiga del material, sino por la deformación permanente del camino de rodadura originada por la carga. Las cargas que actúan sobre un rodamiento estacionario, o sobre un rodamiento que efectúa lentos movimientos de oscilación, así como las cargas de choque que actúan sobre un rodamiento giratorio, pueden dar lugar a superficies aplanadas en los elementos rodantes y a indentaciones en los caminos de rodadura. Estas indentaciones pueden estar distribuidas irregularmente por el camino de rodadura o uniformemente en las posiciones de los elementos rodantes. Si la carga actúa durante varias revoluciones del rodamiento, la deformación se distribuirá por igual por todo el camino de rodadura. Las deformaciones permanentes originadas en el rodamiento pueden dar lugar a vibraciones, ruidos durante el funcionamiento y una mayor fricción. También es posible que aumente el juego interno o que se produzcan cambios en el ajuste.
Estos cambios perjudicarán en mayor o menor medida el rendimiento del rodamiento dependiendo de las exigencias de cada aplicación particular. Por tanto, es necesario garantizar que no se produzcan deformaciones permanentes o que éstas sean muy pequeñas, y para conseguirlo se deberá seleccionar un rodamiento que tenga una capacidad de carga estática lo suficientemente elevada para satisfacer uno de los siguientes requisitos:
alta fiabilidad
funcionamiento silencioso (por ejemplo, en motores eléctricos)
funcionamiento sin vibraciones (por ejemplo, en máquina herramienta)
par de fricción constante del rodamiento (por ejemplo, en aparatos de medición y de realización de pruebas)
baja fricción de arranque bajo carga (por ejemplo, en grúas).
a).- Carga estática equivalente
Las cargas estáticas que tienen componentes radiales y axiales se deben convertir a una carga estática equivalente. Ésta se define como la carga hipotética (radial para los rodamientos radiales y axial para los rodamientos axiales) que, de ser aplicada, causaría en el rodamiento las mismas deformaciones permanentes que la carga real. Se obtiene con la siguiente ecuación general
PO = XOFr + YOFa
Donde:
P0 = carga estática equivalente, kN
Fr = carga radial real del rodamiento (ver el texto que sigue), kN
Fa = carga axial real del rodamiento (ver el texto que sigue), kN
X0 = factor de carga radial del rodamiento
Y0 = factor de carga axial del rodamiento
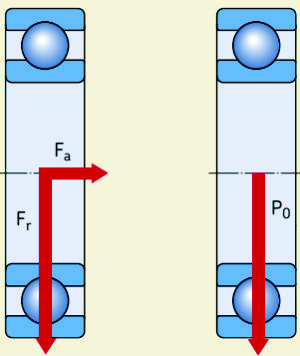
fig. N0 3
Nota.-
Al calcular P0, se deberá utilizar la carga máxima permisible así como sus componentes radiales y axiales (fig. 3) en la ecuación anterior. Si una carga estática actúa sobre el rodamiento en diferentes sentidos, la magnitud de estas componentes cambiará. En estos casos se deberán utilizar las componentes de la carga con el valor máximo de carga estática equivalente P0.
La información y los datos necesarios para calcular la carga estática equivalente de un rodamiento se pueden encontrar en el texto introductorio de cada sección de rodamientos y en las tablas.
b).- Capacidad de carga estática requerida
Cuando el tamaño del rodamiento requerido se determina en base a la capacidad de carga estática, se emplea un factor de seguridad s0, que representa la relación entre la capacidad de carga estática C0 y la carga estática equivalente P0 para calcular la capacidad de carga estática requerida.
La capacidad de carga estática requerida C0 se puede calcular según:
CO = sOPO
Donde:
C0 = capacidad de carga estática, kN
P0 = carga estática equivalente, kN
s0 = factor de seguridad estático
En la tabla 10 se ofrecen valores orientativobasados en la experiencia para el factor de seguridad estático s0, para los rodamientos de bolas y de rodillos en varias aplicaciones que requieren un funcionamiento suave. A temperaturas elevadas, la capacidad de carga estática se reduce. A petición, se facilitará más información.
c).- Comprobación de la capacidad de carga estática
Para los rodamientos cargados dinámicamente y cuando se conozca la carga estática equivalente del rodamiento P0, se recomienda comprobar que la capacidad de carga estática es la adecuada usando:
sO = CO/PO
Si el valor s0 obtenido es menor que el valor orientativo recomendado (tabla 10), se deberá seleccionar un rodamiento con una mayor capacidad de carga estática.
Ejemplos de cálculos
Ejemplo 1
Un rodamiento rígido de bolas SKF Explorer 6309 va a funcionar a 3 000 rpm bajo una carga radial constante Fr = 10 kN. Se va a utilizar una lubricación con aceite, que tendrá una viscosidad cinemática real n = 20 mm2/s a la temperatura de funcionamiento normal. La fiabilidad deseada es del 90 %, y se asume que las condiciones de funcionamiento es limpio. ¿Cuál será la vida nominal básica y de SKF?
Solución
a) La vida nominal básica para una fiabilidad del 90 % es:
![]()
Según las tablas de productos, para un rodamiento 6309, C = 55,3 kN. Al ser la carga puramente radial, P = Fr = 10 kN (“Carga dinámica equivalente del rodamiento”)
L10 = (55,3/10)3 = 169 millones de revoluciones
o en horas de funcionamiento:
![]()
L10h = [1 000 000/(60*3 000)]*169 = 940 horas
b) La vida nominal SKF para una fiabilidad del 90 %:
L10m = a1 aSKF L10
Como se requiere una fiabilidad del 90 %, se deberá calcular la vida L10m y a1 = 1 (tabla 1).
Según las tablas de productos para el rodamiento 6309, dm = 0,5 (d + D) = 0,5 (45 + 100) = 72,5 mm
Según el diagrama 5, el nivel de viscosidad del aceite a la temperatura de funcionamiento para una velocidad de 3 000 rpm,
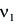 = 8,15 mm2/s. Por tanto,
= 8,15 mm2/s. Por tanto, 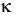 =
= 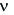 /
/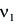 = 20/8,15 = 2,45
= 20/8,15 = 2,45De nuevo, según las tablas de productos Pu = 1,34 kN y Pu/P = 1,34/10 = 0,134. Como las condiciones son de máxima limpieza,
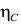 = 0,8 (tabla 4) y
= 0,8 (tabla 4) y 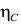 Pu/P = 0,107. Con k = 2,45 y utilizando la escala SKF Explorer del diagrama 1, se obtiene el valor de aSKF = 8. Por tanto, según la fórmula de la vida nominal SKF.
Pu/P = 0,107. Con k = 2,45 y utilizando la escala SKF Explorer del diagrama 1, se obtiene el valor de aSKF = 8. Por tanto, según la fórmula de la vida nominal SKF.
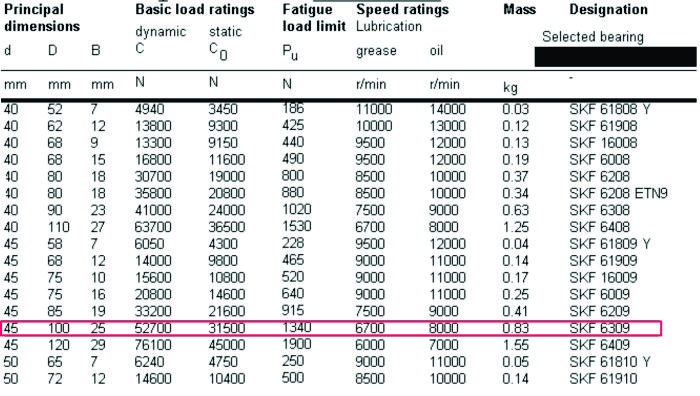
L10m = 1 * 8 * 169 = 1 352 millones de revoluciones
o en horas de funcionamiento usando:
![]()
L10mh = [1 000 000/(60 * 3 000)] * 1 352 = 7 512 horas
Ejemplo 2
El rodamiento rígido de bolas SKF Explorer 6309 del ejemplo 1 pertenece a una aplicación existente calculada hace algunos años usando el
factor de ajuste a23. Esta aplicación cumplía totalmente con las exigencias. Ahora debemos recalcular la vida de este rodamiento en términos del factor de ajuste a23 y también del factor aSKF (según la experiencia de campo de esta aplicación), es decir, aSKF = a23. Por último, debemos obtener el factor ![]() para el nivel de contaminación en la aplicación bajo la condición aSKF = a23.
para el nivel de contaminación en la aplicación bajo la condición aSKF = a23.
Solución
1).- Con k = 2,45, usando la escala a23 superpuesta sobre las curvas k para el factor de ajuste de la vida SKF aSKF del diagrama 1, el factor a23 = 1,8 que podemos leer en el eje aSKF. Teniendo en cuenta que esta aplicación satisfacía totalmente los requisitos, se puede suponer con seguridad que aSKF = a23, y por tanto:
L10mh = a23 L10h = aSKF L10h = 1,8 * 940
L10mh = 1 690 horas de funcionamiento
2).- El factor ![]() correspondiente a este ajuste de vida según la tabla 6 y para un rodamiento SKF Explorer 6309 con Pu/P = 0,134
correspondiente a este ajuste de vida según la tabla 6 y para un rodamiento SKF Explorer 6309 con Pu/P = 0,134
![]() = [
= [![]() (Pu/P)]23/(Pu/P) = 0,04/0,134 = 0,3
(Pu/P)]23/(Pu/P) = 0,04/0,134 = 0,3
Ejemplo 3
Se debe revisar una aplicación existente. Un rodamiento rígido de bolas SKF Explorer 63092RS1 con obturaciones integradas y llenado de grasa, funciona bajo las mismas condiciones descritas en el ejemplo 2 (k = 2,45). Se debe comprobar la contaminación de esta aplicación para determinar si es posible reducir los costes para una vida mínima requerida de 3 000 horas de funcionamiento.
Solución
1).- Teniendo en cuenta la lubricación con grasa y las obturaciones integradas, el nivel de contaminación se puede caracterizar por una limpieza, y según la tabla 4, ![]() = 0,8. Con Pu/P = 0,134;
= 0,8. Con Pu/P = 0,134; ![]() (Pu/P) = 0,107, según la escala SKF Explorer del diagrama 1 y con k = 2,45, aSKF = 8.
(Pu/P) = 0,107, según la escala SKF Explorer del diagrama 1 y con k = 2,45, aSKF = 8.
L10mh = 8 * 940 = 7 520 horas de funcionamiento
2).- Para una versión más económica de la misma disposición, si es posible, se selecciona un rodamiento SKF Explorer 63092Z con placas de protección. El nivel de contaminación se puede considerar como de limpieza normal, y entonces según la tabla 4, ![]() = 0,5. Con Pu/P = 0,134,
= 0,5. Con Pu/P = 0,134, ![]() (Pu/P) = 0,067, según la escala SKF Explorer del diagrama 1, y k = 2,45, aSKF = 3,5.
(Pu/P) = 0,067, según la escala SKF Explorer del diagrama 1, y k = 2,45, aSKF = 3,5.
L10mh = 3,5 * 940 = 3 290 horas de funcionamiento
Conclusión: Si fuese posible, esta aplicación podría beneficiarse de una solución más económica reemplazando el rodamiento obturado por un rodamiento con placas de protección.
Se debe advertir que el uso de la vida nominal basada en el factor de ajuste a23 no permitiría esta evaluación del diseño. Es más, no sería posible alcanzar la vida requerida (ejemplo 2, la vida calculada con un factor de ajuste a23 sólo daría 1 690 horas).
Ejemplo 4
El rodamiento rígido de bolas SKF Explorer 6309 utilizado en el ejemplo 1 pertenece a una aplicación que se calculó hace algunos años usando el factor de ajuste a23. Se han recibido quejas de fallos en el rodamiento. Se requiere evaluar el diseño de la aplicación del rodamiento con el fin de determinar las medidas necesarias para aumentar su fiabilidad.
Solución
1).- En primer lugar, se determina la vida del rodamiento basándose en el factor a23. Con k = 2,45, usando la escala a23 superpuesta sobre las curvas k para el factor de ajuste de la vida SKF aSKF del diagrama 1, a23 = 1,8 que podremos leer en el eje aSKF.
L10mh = a23 * L10h = 1,8 * 940 = 1 690 horas de funcionamiento
2).- El factor hc correspondiente a este factor de ajuste de la vida a23 es, según la tabla 6, y para Pu/P = 0,134
![]() = [
= [![]() (Pu/P)]23/(Pu/P) = 0,04/0,134 = 0,3
(Pu/P)]23/(Pu/P) = 0,04/0,134 = 0,3
3).- Un recuento microscópico de una muestra de aceite tomada de la aplicación señaló una clasificación de contaminación de /17/14 según la normativa ISO 4406:1999. La contaminación consistía principalmente en partículas de desgaste originadas en el sistema. Se puede considerar como “contaminación típica”, y por tanto según la tabla 4 y diagrama 9, ![]() = 0,2. Con Pu/P = 0,134;
= 0,2. Con Pu/P = 0,134; ![]() (Pu/P) = 0,0268 según la escala SKF Explorer en el diagrama 1, y k = 2,45, aSKF = 1,2.
(Pu/P) = 0,0268 según la escala SKF Explorer en el diagrama 1, y k = 2,45, aSKF = 1,2.
L10mh = 1,2 * 940 = 1 130 horas de funcionamiento
4).- Al utilizar un rodamiento SKF Explorer 63092RS1 con obturaciones rozantes integradas, el nivel de contaminación se puede reducir al nivel de “limpieza”. Entonces según la tabla 4, ![]() = 0,8. Con Pu/P = 0,134,
= 0,8. Con Pu/P = 0,134, ![]() (Pu/P) = 0,107 según la escala SKF Explorer en el diagrama 1 y k = 2,45, aSKF = 8.
(Pu/P) = 0,107 según la escala SKF Explorer en el diagrama 1 y k = 2,45, aSKF = 8.
L10mh = 8 * 940 = 7 520 horas de funcionamiento
Conclusión: El nivel de contaminación de esta aplicación es superior al factor ![]() = 0,3 que es el nivel de contaminación implícito cuando se utiliza el factor a23, mientras que las condiciones de funcionamiento reales, típicas para transmisiones industriales contaminadas, requieren un factor
= 0,3 que es el nivel de contaminación implícito cuando se utiliza el factor a23, mientras que las condiciones de funcionamiento reales, típicas para transmisiones industriales contaminadas, requieren un factor ![]() = 0,2 cuando se utiliza el factor aSKF.
= 0,2 cuando se utiliza el factor aSKF.
Esto puede explicar la causa de los fallos experimentados en esta aplicación. El uso de un rodamiento SKF Explorer 63092RS1 con obturaciones rozantes integradas hará que la fiabilidad aumente considerablemente y solucionará el problema.
Ejemplo 5
El ciclo de trabajo de un rodamiento de rodillos a rótula SKF Explorer 240262CS2/VT143 obturado que se utiliza en un equipo de transporte pesado de una acería, tiene las condiciones de funcionamiento que aparecen a continuación.
La carga estática de esta aplicación está determinada con una precisión razonable, teniendo en cuenta la inercia de la carga durante la operación de carga y la presencia de cargas de choque causadas por la caída accidental de cargas.
Se requiere verificar las condiciones de carga dinámica y estática de esta aplicación asumiendo una vida de funcionamiento requerida L10mh de 60 000 horas y un factor de seguridad estáticomínimo de 1,5.
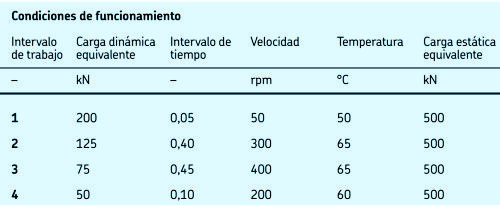
Solución
1).- Según la tabla de productos y la parte teórica:
Capacidad de carga:
C = 540 kN; C0 = 815 kN; Pu = 81,5 kN
Dimensiones:
d = 130 mm; D = 200 mm, entonces dm = 0,5 (130 + 200) = 165 mm
Llenado de grasa:
Grasa de extrema presión con aceite base mineral y un espesante de litio con una consistencia de clase NLGI 2, un margen de temperaturas de –20 a +110 °C, y una viscosidad del aceite base a 40 y 100 °C de 200 y 16 mm2/s, respectivamente.
2).- Se realizan los siguientes cálculos o se determinan los valores:
a).- ![]() = viscosidad requerida, mm2/s (diagrama 5) – datos: dm y velocidad
= viscosidad requerida, mm2/s (diagrama 5) – datos: dm y velocidad
b).- ![]() = viscosidad de funcionamiento real, mm2/s (diagrama 6) – datos: viscosidad del lubricante a 40 °C y temperatura de funcionamiento
= viscosidad de funcionamiento real, mm2/s (diagrama 6) – datos: viscosidad del lubricante a 40 °C y temperatura de funcionamiento
c).- k = relación de viscosidad – calculada (![]() /
/![]() )
)
d).- ![]() = factor para el nivel de contaminación (tabla 4) – “Limpio”, rodamiento obturado:
= factor para el nivel de contaminación (tabla 4) – “Limpio”, rodamiento obturado: ![]() = 0,8
= 0,8
e).- L10h = vida nominal según la fórmula indicada – datos: C, P y n
f).- aSKF = según el diagrama 2 – datos: Rodamiento SKF Explorer, ![]() , Pu, P y k
, Pu, P y k
g).- L10mh1,2, … = Vida nominal SKF según la fórmula – datos: aSKF y L10h1,2, …
h).- L10mh = vida nominal SKF según la fórmula – datos: L10mh1, L10mh2, … y U1, U2, …
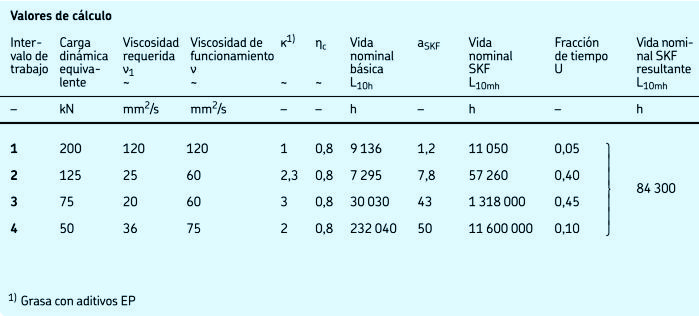
La vida nominal SKF de 84 300 horas es superior a la de la vida útil requerida, y por tanto, se verifican las condiciones de carga dinámica del rodamiento.
Por último, se examina el factor de seguridad estático de esta aplicación
s0 = [CO/PO] = (815/500) = 1.63
s0 = 1,63 > s0 req
La fórmula anterior demuestra que la seguridad estática de esta aplicación está verificada. Como la carga estática se determina de un modo preciso, el margen relativamente pequeño entre la seguridad estática calculada y la recomendada no debe ser preocupante.
3.2.2.4.- Método antiguo(menos preciso)
a).- Vida ütil.
El cálculo de la vida útil es dependiente del rodamiento en particular, esto lo convierte en un cálculo iterativo en el cual se escoge un rodamiento y se comprueba su vida útil, si el resultado es satisfactorio, la selección ha terminado, pero si la vida es menor o muy mayor de lo recomendado debe escogerse otro rodamiento y recalcular la vida.
La vida ütil o duración de un rodamiento se define como el número de revoluciones o de horas a una velocidad constante determinada que el rodamiento puede dar antes de que se manifieste el primer signo de fatiga en uno de sus aros o de sus elementos rodantes.
Las capacidades de carga dinámica están basadas en la duración alcanzada o sobrepazada por el 90% de los rodamientos aparentemete idénticos de un grupo suficientemente grande. A esta duración se le denomina duración nominal.
Las tablas siguientes entregan recomendaciones para la vida útil que debería tener un rodamiento para las aplicaciones que se detallan, este es el punto de partida.
Ver Tablas orientativos de la vida nominal de un rodamiento: Tablas 08 y 09)b).- Procedmiento de cálculo.
Una vez ubicada la vida sugerida, se procede a escoger un rodamiento del catálogo considerando el tipo de carga a soportar y las limitaciones dimensionales del problema. Una vez ubicados algunos candidatos se extraen los valores de C, C0, Pu, D y d. De las condiciones del problema se obtienen el tipo de aceite utilizado, la temperatura de operación, la velocidad del eje, la fiabilidad requerida y el grado de contaminación. Con estos valores se procede a realizar los cálculos que a continuación se detallan.
Ver datos de productos SKF on line
*Carga dinámica equivalente (P): Es una carga hipotética, constante en magnitud y dirección , que si se actuara radialmente sobre un rodamiento radial, o axialmente sobre uno axial; tendría el mismo efecto en la duración, que las cargas reales a las que está sometido el rodamiento. La capacidad de carga (P) depende de las cargas que actúan sobre el rodamiento y de unas constantes del mismo.
En particular, la carga equivalente sobre el rodamiento se obtiene de fórmulas como la siguiente:
P = X Fr + Y Fa
Donde:
Fr es la carga radial que se aplica sobre
el rodamiento
Fa es la carga axial que se aplica sobre el rodamiento
X e Y (factor radial y factor axial) son valores adimensionales que varían para cada tipo de rodamiento.
Por ejemplo, en la tabla siguiente se muestran los valores de estas variables para el caso de rodamientos radiales de bolas con juego normal. Para el cálculo de otro tipo de rodamiento debe consultarse el catálogo de rodamientos en el capítulo correspondiente, para obtener los valores de: e, Y , X.
En los rodamientos radiales de una hilera de bolas o de rodillos, una carga axial adicional no influye en la carga equivalente P para ![]() (usar X=1 y Y=0, para rodamientos rígido de bolas), pero en los rodamientos de dos hileras, pequeñas cargas axiales influyen considerablemente. Cuando
(usar X=1 y Y=0, para rodamientos rígido de bolas), pero en los rodamientos de dos hileras, pequeñas cargas axiales influyen considerablemente. Cuando ![]() (Se recomienda usar X=0.56 y para Y usar grafico, para rodamientos rígido de bolas) o en caso contrario usar la siguiente tabla para hallar X e Y.
(Se recomienda usar X=0.56 y para Y usar grafico, para rodamientos rígido de bolas) o en caso contrario usar la siguiente tabla para hallar X e Y.
Tabla 3.2.4.- Valores de X y Y para los diferentes tipos de rodamientos.
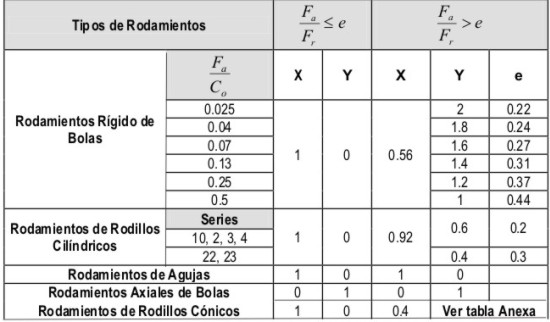
Fuente: Catálogo General SKF
tabla Anexa
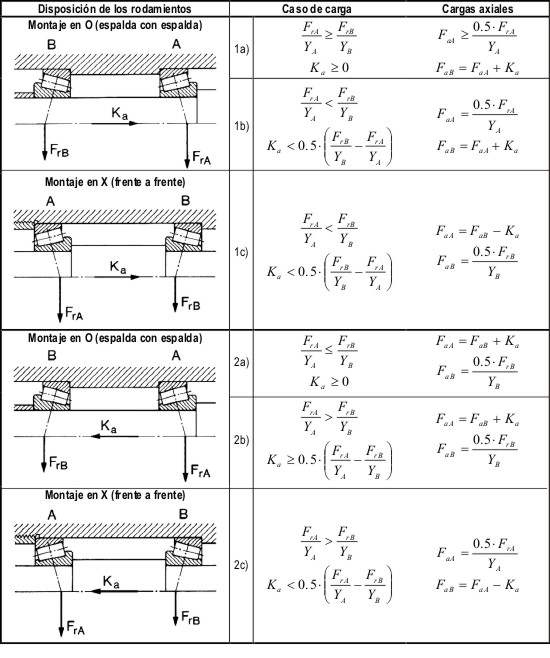
Fuente: Catálogo General SKF
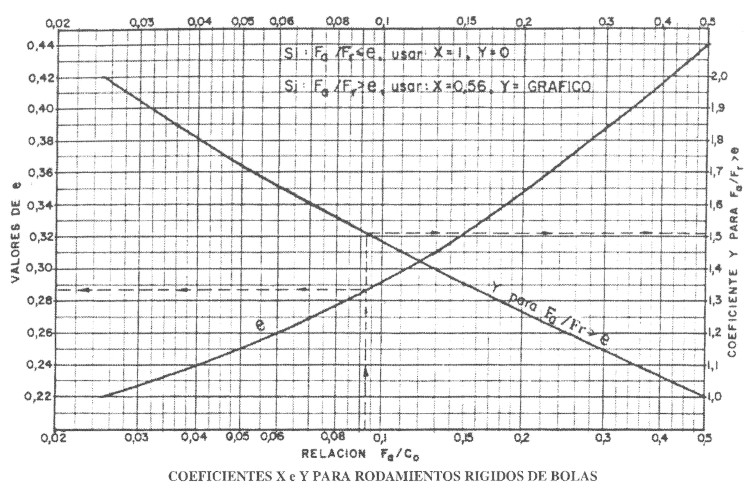
Fuente: Catálogo General SKF
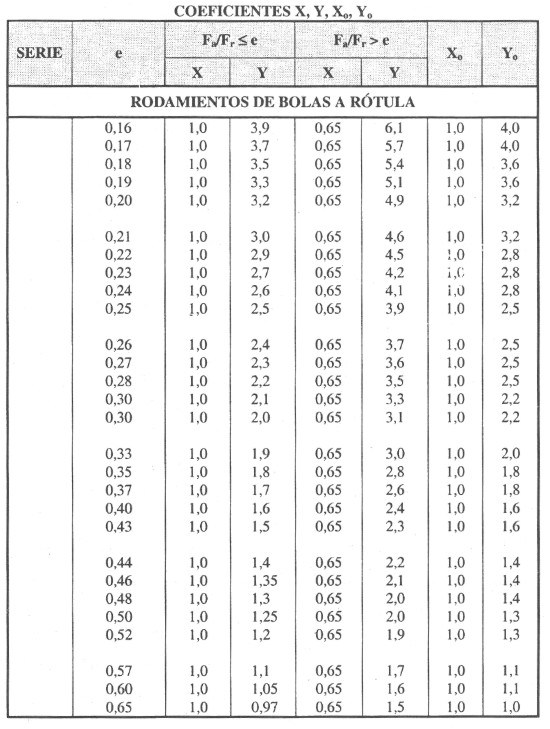
Fuente: Catálogo General SKF
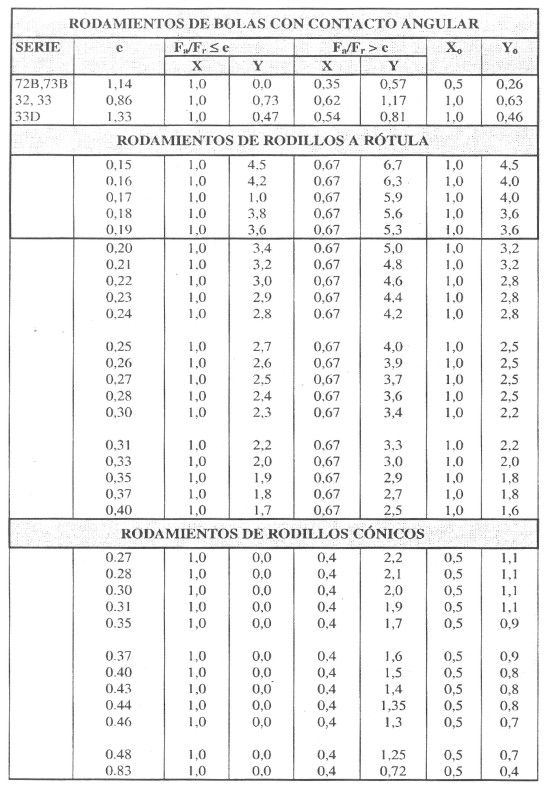
Fuente: Catálogo General SKF
Se desarrollaran tres fórmulas para la vida útil: Vida Nominal [L10]; Vida Nominal Ajustada [Lna] y Vida Nominal Ajustada SKF [Lnaa].
- Vida Nominal (fórmula ISO de la vida nominal):
L10 = ( C / P )p
Donde:
L10 es la vida estimada en millones de
revoluciones
C es la capacidad de carga dinámica
P es la carga equivalente sobre el rodamiento, se calcula en función de las cargas
radiales y axiales que afectan al rodamiento su fórmula depende del tipo de rodamiento a
utilizar
p es 3 para los rodamientos de bolas y 10/3 para los rodamientos de rodillos
La vida nominal puede ser expresarse en otras unidades mas adecuadas al problema que se analiza, de esta forma se tiene:
L10h = ( 1000000 / 60 n ) L10
Donde:
L10h es la vida estimada en horas de
funcionamiento
n es la velocidad del eje en r.p.m.
L10s = ( p D / 1000 )
Donde:/p>
L10s es la vida estimada en millones
kilómetros recorridos
D es el diámetro de las ruedas en metro
- Vida Nominal Ajustada.
Lna = a1 a23 L10
Donde:
a1 es el factor correspondiente a la fiabilidad del rodamiento, este factor se obtiene de la tabla siguiente, se puede observar que la fiabilidad mínima es de 90% y que es imposible asegurar un 100%.
Tabla 3.2.4
Valor del factor a1 |
|
Fiabilidad % |
a1 |
90 |
1 |
95 |
0,62 |
96 |
0,53 |
97 |
0,44 |
98 |
0,33 |
99 |
0,21 |
a23 es un factor que considera la calidad de la lubricación y su obtención requiere el uso de dos gráficos que a continuación se muestran.
Se necesita conocer las dimensiones básicas del rodamiento: su diámetro exterior D y su diámetro interior d. Esto significa que es preciso darse un rodamiento y calcular su vida útil según las condiciones del problema.
Con las dimensiones principales del rodamiento se calcula el promedio dm = ( D + d ) / 2 y se entra al gráfico por el eje horizontal. A continuación se sube hasta tocar la línea inclinada correspondiente a la velocidad de giro del eje en r.p.m. Se sale horizontalmente hasta cortar el eje vertical del gráfico, obteniendo el valor de la viscosidad cinemática n1 requerida por el rodamiento.
Diagrama 1
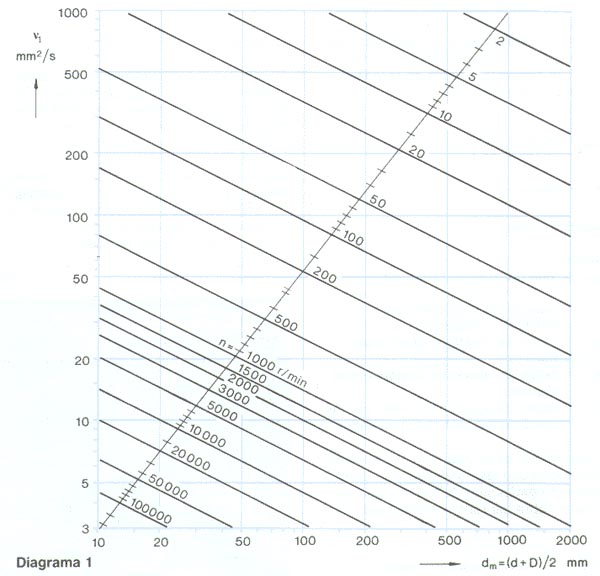
Fuente: Catálogo General SKF
El siguiente gráfico nos entrega la viscosidad cinemática que se tiene en la realidad, considerando el lubricante utilizado y la temperatura de operación. Para iniciar el proceso, se ubica el valor de la viscosidad del lubricante a utilizar en la siguiente tabla.
Tabla 3.2.5
Clase ISO de viscosidad |
Viscosidad cinemática a 40 ºC |
||
media |
mín |
máx |
|
| - | mm2/s |
||
| ISO VG 2 | 2,2 |
1,98 |
2,42 |
| ISO VG 3 | 3,2 |
2,88 |
3,52 |
| ISO VG 5 | 4,6 |
4,14 |
5,06 |
| ISO VG 7 | 6,8 |
6,12 |
7,48 |
| ISO VG 10 | 10 |
9,00 |
11,0 |
| ISO VG 15 | 15 |
13,5 |
16,5 |
| ISO VG 22 | 22 |
19,8 |
24,2 |
| ISO VG 32 | 32 |
28,8 |
35,2 |
| ISO VG 46 | 46 |
41,4 |
50,6 |
| ISO VG 68 | 68 |
61,2 |
74,8 |
| ISO VG 100 | 100 |
90,0 |
110 |
| ISO VG 150 | 150 |
135 |
165 |
| ISO VG 220 | 220 |
198 |
242 |
| ISO VG 320 | 320 |
288 |
352 |
| ISO VG 460 | 460 |
414 |
506 |
| ISO VG 680 | 680 |
612 |
748 |
| ISO VG 1 000 | 1 000 |
900 |
1 100 |
| ISO VG 1 500 | 1 500 |
1 350 |
1 650 |
Conocida la viscosidad se observa que este valor se entrega para una temperatura de referencia de 40ºC, por ello, se ubica en el gráfico siguiente la línea vertical que representa 40ºC y sobre ella se ubica la viscosidad nominal del aceite utilizado. Realizado esto, se mueve sobre una línea inclinada paralela a las líneas inclinadas que se muestran en el gráfico hasta cortar con la temperatura de operación de la maquina. Una vez ubicado el punto en cuestión se lee en el eje vertical la viscosidad cinemática n de que se dispone. Por ejemplo un aceite ISO VG 68 tiene una viscosidad media de 68 mm2/s a 40ºC, si la temperatura sube a 70 ºC la viscosidad media desciende a 19 mm2/s aproximadamente, si en cambio, la temperatura baja a 30ºC, la viscosidad media sube a 115 mm2/s aproximadamente.
Diagrama 2
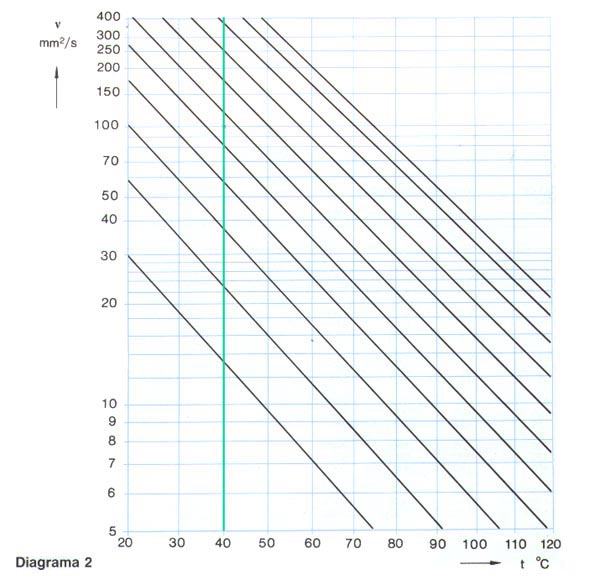
Finalmente en el gráfico que sigue a continuación se
ingresa por el eje horizontal con
K = n / n1 hasta cortar la línea
quebrada y se lee en el eje vertical el valor del factor a23.
Diagrama 3
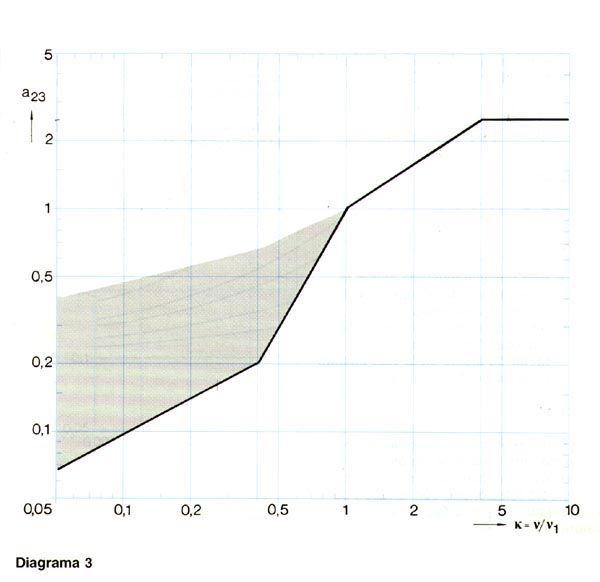
La zona sombreada que aparece el gráfico anterior corresponde a una zona alcanzable con la aplicación de aditivos al aceite.
- Vida Nominal Ajustada SKF.
Lnaa = a1 aSKF L10
Donde:
a1 es el factor de confiabilidad
utilizado en el calculo anterior
aSKF es un nuevo factor introducido por la fabrica SKF. Para conocer su valor se debe primeramente evaluar el valor hc que varia en función al grado de contaminación, este valor se puede obtener de la tabla siguiente:
Tabla 3.2.6
Valores del factor de ajuste hc para diferentes grados de contaminación |
|
| Condición1) | hc |
| Muy limpio
Tamaño de partículas del orden del espesor de la película de lubricante. |
1 |
| Limpio
Condiciones típicas de rodamientos con obturaciones engrasados por vida. |
0,8 |
| Normal
Condiciones típicas de rodamientos con protecciones engrasados por vida. |
0,5 |
| Contaminado
Condiciones típicas de rodamientos sin obturaciones integradas; filtros de paso grueso paras lubricante y/o entrada de partículas desde el entorno. |
0,5 a 0,1 |
| Fuertemente contaminado2) | 0 |
|
|
Fuente: Catálogo General SKF
Ahora se requiere el valor de Pu (Carga límite de fatiga) obtenido del catalogo para el rodamiento en cuestión y el valor de la carga equivalente P obtenido de las condiciones del problema.
Con todo esto de evalúa (hc Pu / P ) y se ingresa por el eje horizontal en uno de los cuatro gráficos que siguen a continuación.
Obtenido el valor aSKF se procede a evaluar Lnaa . De esta forma se han obtenido 3 resultados para la vida útil del rodamiento.
El proceso de cálculo se representa en el siguiente esquema:

Para el caso de cargas fluctuantes que afecten al rodamiento es recomendable que se consulte el catalogo de rodamiento para fórmulas mas complejas. En la confección de este apunte se ha utilizado el "Catálogo General de Rodamientos SKF" que contiene además mucha información relevante.

3.2.3.- Otras selecciónes.
|
Fig. 3.2.3 |
Existen muchas aplicaciones que requieren un rodamiento de diseño especial. Una de esta situaciones es la falta de espacio para colocar un rodamiento normal. Para ofrecer un solución a este problema, se crean los rodamientos de agujas, que consisten en cilindros delgados unidos por un canastillo o jaula y el aro exterior. La carencia de aro interior y el reducido diámetro de las agujas, logra un rodamiento delgado con aspecto de anillo. Para situaciones en donde el espacio es aún mas reducido, existen rodamientos sin aro exterior que se denominan "corona de agujas" y rodamientos denominados "casquillos de agujas" compuestos por agujas y un aro exterior de acero delgado.
|
|
Fig. 3.2.4 |
Los rodamientos de agujas también se aplican para cargas axiales en donde las agujas (o mas exactamente los troncos de cono) se ordenan en un canastillo y puede tener aros de variados espesores, aprovechando el espacio disponible.
|
|
Fig. 3.2.5 |
Cuando se realiza el diseño de un montaje, se pueden usar soportes completos que incluyen el rodamiento, los sellos y una base de apoyo que puede ser "de pie" con dos perforaciones para unirlos a una estructura o de "brida" para unirse a una plancha. En la figura se aprecian dos soportes de pie y uno brida del tipo SY que además son a rótula.
|
|
Fig. 3.2.6 |
Finalmente, en la figura se aprecian dos rodamientos lineales, utilizados para el desplazamiento de un objetos a lo largo de un riel. El rodamiento partido es para desplazamientos lineales y el rodamiento entero puede utilizarse para desplazamiento lineal y rotacional.
|
Ver: Glosario de rodamientos SKF.
Ver: Sistema de selección de productos y de asesoramiento INA - FAG online.