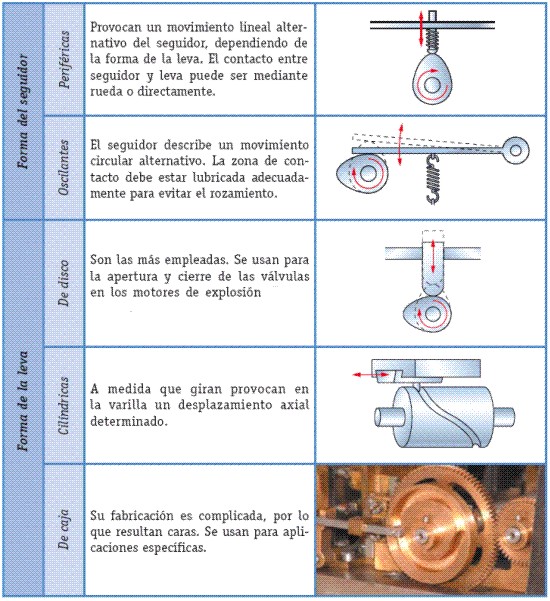
5.- Levas.
5.1.- Introducción.
|
LEVA |
Tipos:
Levas lineales.- Tienen muy pocas aplicaciones.
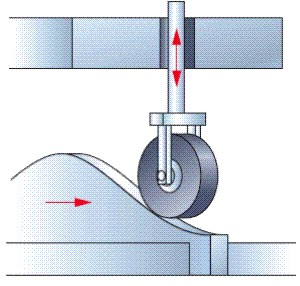
Fig. 4.1
Levas rotativas.- El desplazamiento máximo que sufre el seguidor se conoce como alzada de la leva. El retorno del seguidor se puede hacer por gravedad o mediante muelle. Dependiendo de la forma y del funcionamiento del seguidor, las levas se clasifican en los tipos indicados en la tabla 4.1.1
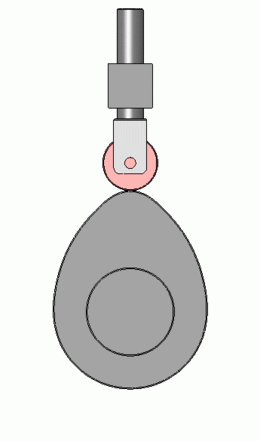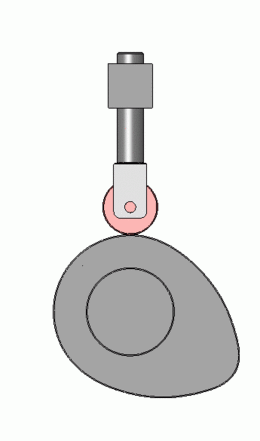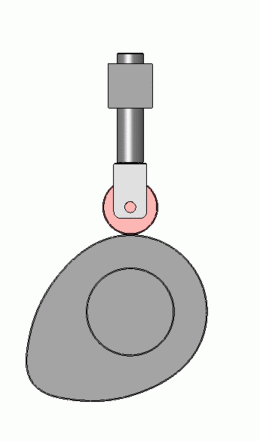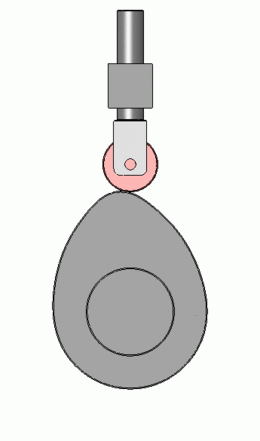
Fig. 4.2
|
Tabla 4.1.1
|
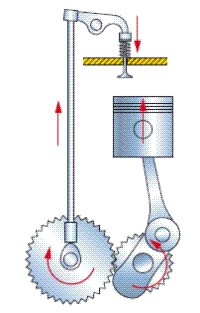
Esquema del funcionamiento de apertura y cierre de las válvulas de un motor de combustión interna. Fig. 4.3 |
5.2.- Leva de disco y rueda de contacto.
Una leva es un elemento que impulsa, por contacto directo, a otro elemento denominado seguidor de forma que éste último realice un movimiento alternativo concreto. Aunque existen muchos tipos de mecanismos de leva, uno de los más comunes es el mecanismo de leva con seguidor de rodillo que se presenta a continuación.
Pese a que tanto la leva como el seguidor pueden disfrutar de un movimiento de rotación o de traslación, el caso más habitual es que la leva gire mientras que el seguidor se desplaza. En este tipo de mecanismo, el objetivo es relacionar de forma precisa la rotación de la leva (cuya posición viene definida por el ángulo de leva "q") con el movimiento del seguidor (cuya posición viene definida por la elevación "y" del mismo). Así, el punto de partida para el diseño de una leva es lo que se conoce con el nombre de diagrama de elevación, que representa con precisión la elevación del seguidor para cada posición angular de la leva. Este diagrama constituye la representación gráfica de la función y(q), variando q entre 0º y 360º.
Hay que decir, que la elevación y se mide siempre respecto de la posición más baja del seguidor. Es decir, en la posición más baja se cumple siempre que y = 0.
Aparte de los conceptos definidos hasta ahora, hay otros de especial importancia en el diseño de un mecanismo leva seguidor. Todos estos conceptos pueden ser comprobados en la figura siguiente.
-
Rodillo: Para evitar el rozamiento que se produciría entre la leva y el seguidor si éstos contactaran directamente, se introduce entre ambos un rodillo que cambia el tipo de contacto a rodadura pura (en condiciones ideales). El rodillo está articulado al seguidor en su extremo y rueda sobre la leva (ver figura a continuación).
-
Punto de trazo: Al incluir el rodillo, el seguidor no contacta directamente con la leva, sino que contacta con el rodillo y éste con la leva. El punto de trazo es el punto del seguidor alrededor del cual gira el rodillo. Es, por tanto, el punto extremo del seguidor que estaría en contacto con la leva si no hubiese rodillo (ver figura a continuación).
-
Curva primitiva: Es la curva que definiría el perfil de la leva si no hubiese rodillo. Es, también, la curva por la que pasa el punto de trazo al moverse la leva. De hecho, durante el diseño de la leva, partiendo del diagrama de elevación se obtiene la curva primitiva (o primera forma de la leva). Posteriormente, esta curva se reduce en una cantidad igual al radio del rodillo que se desea colocar (ver figura a continuación).
-
Círculo primario: Es el menor círculo que se puede dibujar centrado en el centro de rotación de la leva y tocando la curva primitiva. Así, el círculo primario toca punto de trazo sólo cuando el seguidor se encuentra en la posición más baja posible. El tamaño del círculo primario debe decidirse en el momento de comenzar a diseñar la leva y su magnitud influye sobre el tamaño final de la leva, como se verá más adelante.
En la siguiente figura puede observarse el movimiento de la leva y su relación con el diagrama de elevación. En él, la flecha azul sobre la leva constituye una referencia que indica la rotación de la misma. El movimiento puede accionarse automáticamente pulsando el botón "Mov. Auto" o bien manualmente arrastrando con el ratón el cuadrado situado en el extremo de la flecha azul. Durante el movimiento, verificar:
-
que el sistema leva-seguidor cumple perfectamente con el diagrama de elevación mostrado, ya que la leva se ha diseñado para ello,
-
que el punto de trazo sigue siempre la curva primitiva,
-
que el punto de trazo toca el círculo primario solamente cuando el seguidor está en su posición más baja y
-
que el perfil de la leva dista de la curva primitiva, en todos los puntos, una distancia igual al radio del rodillo.
Excentricidad
En ocasciones resulta interesante desplazar el seguidor de forma que su dirección de deslizamiento no pase por el centro de rotación de la leva. En este caso, se dice que el seguidor es excéntrico y se llama excentricidad a la distancia desde el centro de rotación de la leva a la dirección de deslizamiento del seguidor. La circunferencia centrada en el centro de rotación de la leva y tangente a la dirección de deslizamiento del seguidor se denomina circunferencia de excentricidad.
Nótese por comparacíon de la figura siguiente con la anterior que, sin cambiar el diagrama de elevación ni ningún otro parámetro de diseño de la leva, al dotar al seguidor de cierta excentricidad la forma de la leva cambia (y no solo cambia su orientación) llegando a ser asimétrica pese a la simetría del diagrama de elevación. También cambian otros factores importantes, como el ángulo de presión, que se estudiará más adelante.
Pausa del seguidor
En ocasiones, los mecanismos de leva son seleccionados porque proporcionan en el seguidor un movimiento intermitente (difícil de conseguir con mecanismos de barras). Así, el movimiento del seguidor es tal que durante un tiempo permanece detenido (pausa ) pero posee movimiento el resto del tiempo. En la siguiente figura se muestra sistema leva-seguidor con pausa en la mínima elevación. Obsérvese la pausa en el diagrama de elevación y cómo ésta se encuentra en la posición más baja del seguidor. Obsérvese también durante el movimiento de la leva que el tramo de perfil de leva que produce la pausa en el seguidor es un arco de circunferencia centrado en el centro de rotación de la leva.
Los mecanismos leva-seguidor se pueden diseñar también para poseer más de una pausa. En el ejemplo mostrado a continuación, el seguidor cuenta con dos pausas, una en la elevació máxima y otra en la elevación mínima. Obsérvese cómo una pausa de seguidor corresponde siempre en la leva giratoria con un arco de circunferencia centrado en el centro de rotación de la misma.
Ángulo de presión
El ángulo de presión es un parámetro fundamental en el comportamiento dinámico de las levas. Se define como el ángulo que forman dos rectas: la línea de deslizamiento del seguidor y la recta normal a las dos superficies (leva y rodillo) en el punto de contacto.
Dos curvas (o superficies) que contactan en un punto poseen siempre una tangente común en el punto de contacto. La recta normal es, precisamente, la perpendicular a la tangente en dicho punto. En todo contacto sin rozamiento, las fuerzas que se transmiten desde una curva (o superficie) a la otra a través del contacto tienen siempre la dirección de la normal. Por este motivo, cuando la leva empuja al seguidor hacia arriba no lo hace siempre mediante una fuerza vertical, sino que lo hace mediante una fuerza que sigue la dirección de la normal. Dicha fuerza tendrá una componente vertical que es útil para el movimiento, pero también tendrá una componente horizontal (inútil) que tiende a deformar el seguidor por flexión y que incrementa el rozamiento en el par de deslizamiento del seguidor. Si el ángulo de presión es grande, para una misma componente vertical (útil), la componente horizontal (inútil) será grande.
El problema es que el ángulo de presión depende de la posición de la leva (no es constante todo el tiempo) y, para que el sistema tenga un buen comportamiento dinámico, se intenta siempre que el ángulo de presión máximo no supere cierto valor (alrededor de los 30º). Dicho valor máximo dependerá del tamaño de la leva, como se verá más adelante.
En la siguiente animación se observa el gráfico de variación del ángulo de presión en función del ángulo que ha girado la leva.
Influencia del tamaño del círculo primario
El radio del círculo primario es, junto con otros, un parámetro de diseño que debe ser decidido antes de comenzar a diseñar la leva. Su valor influye fundamentalmente en dos importantes aspectos: el tamaño de la leva y el ángulo de presión.
Cuando el círculo primario crece, el tamaño de la leva crece. Desde este punto de vista, es recomendable emplear círculos primarios pequeños ya que de esta forma se consiguen mecanismos leva-seguidor compactos.
Sin embargo, al disminuir el radio del círculo primario, los ángulos de presión crecen, lo que aumenta la componente de la fuerza de contacto que es perpendicular al seguidor (y que es, por tanto, inútil). Esta componente perpendicular genera problemas importantes por lo que su valor debe mantenerse bajo (en general se considera aceptable por debajo de 30º). Así, desde el punto de vista de ángulo de presión, el círculo primario debería ser lo más grande posible.
La solución final será un compromiso entre obtener un diseño compacto y mantener ángulos de presión suficientemente bajos.
La animación siguiente muestra la influencia del tamaño del círculo primario en el sistema leva-seguidor. En ella se muestra la gráfica del diagrama de elevación y también la gráfica de evolución del ángulo de presión. Nótese que, sin cambiar ningún otro parámetro del sistema, el ángulo de presión crece al variar el tamaño del círculo primario (puede realizarse mediante la barra de desplazamiento) en cualquier posición (salvo las de reposo del seguidor).
Influencia de la excentricidad
La excentricidad es otro parámetro de partida en el diseño de sistemas leva-seguidor. Su valor no puede ser mayor el radio del círculo primario ya que, si así fuera, habría al menos una posición en la que el seguidor caería por falta de contacto con la leva.
La excentricidad influye sobre todo en el ángulo de presión. Sin embargo, no modifica la forma de la gráfica de variación del ángulo de presión, sino que solamente la desplaza verticalmente. Así, la excentricidad puede hacer que disminuya el ángulo de presión en unas zonas del diagrama de elevación a costa de aumentar en otras zonas. Además, la excentricidad hace que el ángulo de presión deje de ser nulo cuando el seguidor está en pausa.
En la práctica, el seguidor se suele mantener en contacto con la leva por la acción de un muelle que lo presiona contra la leva. Por eso, habitualmente la fuerza de contacto es mayor durante el ascenso del seguidor (en el que la leva ha de vencer la fuerza del muelle) que en el descenso (en el que la acción del muelle ayuda a que la leva siga girando, contribuyendo a la continuación del movimiento). Por este motivo, es más importante obtener un ángulo de presión menor durante el ascenso. Así, a muchos mecanismos leva-seguidor se les suele proporcionar una pequeña excentricidad destinada a disminuir el ángulo de presión durante el ascenso aunque éste crezca durante el descenso.
En la animación siguiente se puede observar la influencia de la excentricidad en el ángulo de presión. Obsérvese cómo varía la gráfica del ángulo de presión al variar la excentricidad (mediante la barra de desplazamiento). Trátese de dotar al mecanismo de una cierta excentricidad destinada a disminuir un poco el ángulo de presión máximo durante el ascenso. Obsérvese cómo efectivamente el ángulo de presión crece durante el descenso. Obsérvese también que al dotar al mecanismo de cierta excentricidad, el ángulo de presión deja de ser nulo cuando el seguidor está en pausa.
Influencia del tamaño del rodillo
El tamaño del rodillo solamente influye en el tamaño relativo del rodillo y de la leva. No influye en el ángulo de presión, por lo que no es un parámetro fundamental desde el punto de vista de comportamiento dinámico del sistema.
En la animación siguiente puede observarse la influencia del tamaño del rodillo, variando su radio mediante la barra de desplazamiento. Obsérvese que ni la curva primitiva ni la gráfica de variación del ángulo de presión cambian.
Sin embargo, para cada leva (definida por su diagrama de elevación, por el radio del círculo primario y por la excentricidad) existe un tamaño máximo de rodillo. Por encima de este tamaño máximo, el perfil de leva degenera y solamente es posible en teoría (en la práctica no es construible). Así, el tamaño del rodillo debe mantenerse en un tamaño suficientemente pequeño para que no se produzca degeneración en el perfil de la leva ni éste presente picos (el radio de rodillo máximo admisible depende del radio de curvatura mínimo de la curva primitiva).
En la siguiente animación se muestra cómo el perfil de la leva puede llegar a degenerar al aumentar mucho el radio del rodillo.
Problema de despegue en levas
Uno de los problemas principales de algunos mecanismos leva- seguidor es el problema de despegue del seguidor debido a los efectos dinámicos del movimiento. En muchos casos, el contacto entre la leva y el seguidor se consigue mediante un resorte (o muelle) que presiona el seguidor contra la leva, tal como muestra la figura siguiente. Durante el ascenso el seguidor sufre una primera fase de aceleración y luego otra de deceleración. Debido a su inercia el seguidor tendrá a seguir subiendo al final de la subida (despegándose de la leva) y es el muelle el encargado de oponerse a esta tendencia, asegurando el contacto con la leva. Así, pues, el problema tiene tres variables fundamentales.
Masa del seguidor: cuanto más pesado sea el seguidor, mayor será su inercia y, por tanto, mayor será la tendencia de éste a despegarse al final de la subida.
Rigidez del muelle: cuanto mayor sea la rigidez del muelle, más fuerza ejerce éste sobre el seguidor para que no se separe de la leva, por lo que la tendencia al despegue será menor.
Velocidad de la leva: cuanto mayor sea la velocidad de la leva, la aceleración y deceleración del seguidor durante la subida será también mayor (el seguidor sube en menos tiempo) y, por tanto, la inercia del mismo será mayor, por lo que la tendencia a despegarse también será mayor.
En conclusión, para que no haya despegue, cuanto mayor sea la velocidad de operación de la leva, menos masa deberá tener el seguidor y mayor deberá ser la rigidez del muelle. El problema es que, aligerar el seguidor puede tener un efecto negativo en su resistencia, y aumentar la rigidez del muelle implica aumentar mucho las fuerza de contacto, por lo que el movimiento de la leva sufrirá una irregularidad mayor ya que durante la subida la gran fuerza de contacto se opone al movimiento, pero lo favorece a la bajada.
El efecto de estas tras variables fundamentales puede experimentarse en la siguiente animación, que constituye un modelo cinetoestático del problema (la velocidad de la leva es constante, es decir, supone que la fuerza de contacto no afecta al movimiento de la leva).